Numerical Approach for Air Temperature,  Soil Temperature and the Difference between Them with Julian Date under Napa Cabbage

Kicheol Eom

doi:10.7745/KJSSF.2023.56.4.419

Preview

Original research article

Korean Journal of Soil Science and Fertilizer. 30 November 2023. 419-430
https://doi.org/10.7745/KJSSF.2023.56.4.419

Numerical Approach for Air Temperature, Soil Temperature and the Difference between Them with Julian Date under Napa Cabbage

Kicheol Eom¹^*

¹Director, SEjong Data Research Institute, Suwon 16432, Korea

^{*Corresponding Author}

ABSTRACT

The main objective of this study was to develop the estimation models for air temperature (Ta), soil temperature (Ts) at 15 cm depth and the difference (dT = Ta - Ts) in Sandy Loam under Napa Cabbage cultivation. The verification process was based on the error analysis criteria. Results indicated a positive correlation between Ta and Ts, with higher Ta corresponding to higher Ts. The estimation models for Ta and Ts according to Julian date were developed as a log functions (log model for Ta, LMTa; log model for Ts, LMTs) judged ｢Fit｣ and ｢Fit well｣, respectively. The linear regressions for Ts and dT as the LRMTs (linear regression model for Ts) and LRMdT (linear regression model for dT) judged ｢Fit｣ and ｢Unfit｣, respectively. Furthermore, an analysis revealed that higher Ta, combined with lower water content, led to an increase in dT. A double regression model for dT, considering both Ta and Qv (double regression model for dT, DRMdT), was found to be a good fit for the dataset. In summary, this study successfully developed estimation models for Ta, Ts, and dT, employing both logarithmic and linear regression approaches. The models were rigorously evaluated using error analysis criteria, providing valuable insights into temperature dynamics in Sandy Loam during Napa Cabbage cultivation.

https://cdn.apub.kr/journalsite/sites/ksssf/2023-056-04/N0230560412/images/ksssf_2023_564_419_F0.jpg

Relationship between measured and estimated value by the DRMdT (double regression model for dT) for the difference (dT = Ta - Ts).

Keywords

Double linear regression model

Linear regression model

Log function model

Model verification

Relative sensitivity

MAIN

Introduction
Materials and Methods
재료 및 방법
Results and Discussion
가을배추 재배 기간의 기온과 토양온도 변화양상 및 시계열 변화 추정모형 설정
기온에 대한 토양온도 및 온도 차이 추정모형 설정
기온과 토양수분 함량에 의한 온도 차이 추정모형 설정
Conclusions

Introduction

토양 분야뿐 아니라 농업 환경 및 기후변화 분야 연구에서 온도 요인은 대단히 중요한 요인이다 (Watson and Challinor, 2013; Kim et al., 2014). 기온 (Ta)뿐 아니라 토양온도 (Ts) 역시 농업 환경 변화의 중요한 지표 (indicator) 중 하나이며, Ts는 식물생육과 토양수분에 큰 영향을 미친다 (Li et al., 2018; Urqueta et al., 2018; Chi et al., 2020). 따라서 Ts는 토양수분과 식물의 농업적 한발을 예측하는 데도 이용되고 있다 (Muro et al., 2018; Ferreira and Duarte, 2019). Ts는 불포화 토양의 작용에 결정적인 영향을 미친다는 많은 연구가 있고 (Delage, 2013; Thota and Vahedifard, 2021; Hashemi et al., 2022; Pham and Sutman, 2023; Pham et al., 2023), 토양 경도에 미치는 Ts의 영향 연구 (Garcia et al., 2023), 토양 호흡에 미치는 Ts의 영향 연구 (Lloyd and Taylor, 1994; Ning et al., 2020) 등이 있으며, 특히, 작물 생육에 미치는 영향은 Ta보다 Ts가 더 크다는 연구 결과도 있다 (Chakraborty et al., 2021). Ts는 기상뿐 아니라 토양수분 함량 (Qv), 식생 등에 따라 종합적으로 변화하지만, Ta가 Ts 변화에 영향을 미치는 가장 중요한 인자라는 연구 결과 (Smith et al., 2010)가 있으며, Kang et al. (2000)은 Ta과 Ts는 깊은 상관관계가 있다 라고 하였다. 따라서 Ta가 변하면 Ts도 이에 영향을 받아 변하게 되므로 Ta 변화에 대하여 Ts는 어떻게 변하는지 구명할 필요가 있다. 그러나 이들을 측정한 원 데이터 (raw data) 또는 상관 분석 등에 의하여 개략적인 변화성은 파악이 되지만, 이들만 가지고는 온도의 변화성을 계량적으로 산정하기 어려우므로, 모델링 (modeling)이라는 과정을 통하여 실측치에 근거한 추정모형을 설정하고 설정된 모형을 분석하여 그 변동성을 계량적으로 파악할 수 있으므로 온도 변화와 관련한 모델링 연구가 많이 수행되고 있다 (Derradji and Aiche, 2014; Fu et al., 2018; Islam et al., 2021). 그러나 대부분은 Ta 및 Ts에 관한 연구 결과이었으며, Ta와 Ts의 온도 차이 (dT = Ta - Ts)에 관한 연구 결과는 찾아보기 어려웠다. 온도 변화 관련 연구에서 Ta 및 Ts 그 자체도 중요한 요인이지만, 상대적인 온도 개념인 dT 역시 중요한 요인이라고 사료 된다. 따라서 본 연구에서는 Ta 및 Ts 뿐만 아니라 dT에 대한 모델링을 수행하였다. 또한, 어떤 물체의 온도 등을 측정할 경우 그 측정치와 모형에 의한 추정치는 오차를 포함하고 있다. 이 오차가 참값과 어느 정도 변이를 나타내는가를 판단하는 것이 정확도 (accuracy) 분석이나 자연현상의 측정에는 대부분 경우 진정한 참값을 알 수 없으므로, 모형에 의한 추정치가 실측치와 비교하여 어느 정도 오차를 포함하고 있는가에 근거하여 그 모형의 적절성 (fitness)을 판단하게 된다. 일반적으로 모형의 적절성은 다음과 같은 세 가지의 관점 (Liemohn et al., 2021)에서 판단하게 된다. 첫째, 정확도 (accuracy)의 관점이다. 이를 판단하는 지표로서는 평균제곱근 편차 (root mean square error, RMSE: Wang and Li, 2010; Zhang et al., 2021), Nash & Sutcliffe 계수 (NSE: Nash and Sutcliffe, 1970) 등이 주로 사용되고 있다. 본 연구에서는 RMSE를 정확도의 지표로 삼고 산출하였다. 둘째, 상호관련성 (association) 관점이다. 변량 간의 상관관계를 분석하여 결정계수 (coefficient of determination: R²)를 지표로 삼아 통계적 유의성이 인정되는가를 판단하게 된다. 하지만 모형의 검증을 위해서 R² 하나에만 근거하여 모형의 적절성을 판단하는 것은 올바른 모형검증이라고 할 수 없다 (Legates and Mc Cabe, 1999; Krause et al., 2005). 셋째, 정밀도 (precision)의 관점이다. 정밀도 분석은 오차 분석 이론에 바탕을 두고 상대정밀도 (relative sensitivity, RS)를 지표로 삼으며 (Mandel, 1964; Shein et al., 2013), 모형에 의한 추정치 표준편차 (standard deviation, STD)의 실측치 STD에 대한 비율인 실측치 기준 표준편차 비율 (ratio of standard deviation, RSTD)을 지표로 삼기도 한다 (Liemohn et al., 2021). 본 연구에서는 RSTD와 RS 두 가지를 정밀도의 지표로 삼고 산출하였다. 본 연구는 가을배추 재배 포장에서 Ta, Ts 및 Qv를 측정하고, Ta 및 Ts 변화에 대한 시계열 분석을 수행함과 동시에 Ta 및 Qv 변화에 따른 Ts와 dT의 변화양상을 분석하고, 이들에 대한 적절한 추정모형 (model)의 함수 형태를 선정하고 최소제곱법에 따라 오차가 최소인 계수를 산정하여 모형을 설정하였으며, 각 추정모형의 RMSE, R², RSTD, RS 등을 산출하여 모형의 적절성을 검증하고, 설정된 모형들을 분석하여 Ta, Ts 및 dT의 변동성을 구명코자 실시하였다.

Materials and Methods

재료 및 방법

본 연구는 전라북도 완주군 이서면 반교리 707-19 농촌진흥청 국립원예특작과학원 시험 포장 (동경 147.033677도, 위도 35.840791도)에 가을배추 (품종명: 청명 가을)를 2022년 9월 7일 정식하여 11월 16일 수확하였다. 자연 강우에 의존하는 무관개 재배하면서 배추 생육 이랑은 흑색 비닐을, 고랑은 흑색 부직포를 멀칭하였다. 가을배추 포장의 토성은 사양토 (sandy loam, SL)이었다. Ta는 기상장치 (ENCOSYS, W. W. Norton & Company, USA)와 Data logger (DT80 Series4, W W Norton & Company, USA)를 통하여 5분 간격으로 실시간 자동 측정된 데이터 중 매일 10:00의 Ta (°C)을 이용하였다. 가을배추 재배 포장의 Ts (°C)를 측정하기 위한 센서 (TEROS21, T21G20010849, METER, USA) 및 Qv (m³ m^-3, %)를 측정하기 위한 센서 (TEROS12, T12-00109142, METER, USA)를 지하 15 cm에 설치하였고 Data logger (ZL6 series, ZENTRA Cloud, METER, USA)를 통하여 10분 간격으로 자동 수집한 후 무선통신 시스템을 이용하여 Serve에 송신된 데이터를 이용하였다. 본 연구에 사용된 데이터는 2022년 9월 16일부터 2022년 11월 16일까지 Ts가 일 평균 Ts에 가장 근접하는 범위에 해당되는 시각인 10:00 (Eom et al., 1990)의 Ta, Ts 및 Qv를 연구 대상으로 삼았다.

Ta과 Ts의 시계열 변화에 대하여 온도의 변화양상이 계속 낮아지는 기간이므로 독립 구간이라는 관점에서 그 추정모형을 각각 Eq. 1 및 Eq. 2와 같이 로그 (ln) 함수 형태인 LMTa (log model for Ta) 및 LMTs (log model for Ts))로 선정하고 최소제곱법에 따라 오차가 최소인 계수를 산정하였다.

(Eq. 1)

LMTa : Ta = a \cdot \ln (JD) + b

(Eq. 2)

LMTs : Ts = c \cdot \ln (JD) + d

여기서, JD : Julian date

a, b, c, d : 계수

Ta와 Ts 및 dT의 각각 직선 회귀 식 (linear regressions: Eq. 3 및 Eq. 4)을 Ts 추정모형 (linear regression model for Ts, LRMTs) 및 dT의 추정모형 (lenear regression model for dT, LRMdT)으로 선정하고 최소제곱법에 따라 오차가 최소인 계수를 산정하였다.

(Eq. 3)

LRMTs : Ts = a \cdot T a + b

(Eq. 4)

LRMdT : dT = c \cdot Ta + d

여기서, a, b, c, d : 계수

Ta과 Qv 두 개의 독립변수를 채택한 이중 회귀 식 (Eq. 5)을 dT의 추정모형 (double regression model for dT, DRMdT)으로 선정하고 최소제곱법에 따라 오차가 최소인 계수를 산정하였다.

(Eq. 5)

DRMdT : dT = Yo + a \cdot Ta + b \cdot Qv

여기서, Yo, a, b : 계수

모형검증을 위한 지표로 삼은 RMSE는 Eq. 6, RMSE의 실측치 STD에 대한 비율인 실측치 기준 RMSE 비율 (the ratio of RMSE to STD of measurement, RRMSEM)은 Eq. 7, RMSE의 모형에 의한 추정치 STD에 대한 비율인 추정치 기준 RMSE 비율 (the ratio of RMSE to STD of estimation, RRMSEE)는 Eq. 8, RSTD는 Eq. 9와 같이 산정하였다 (Moriasi et al., 2007; Naseri et al., 2021).

(Eq. 6)

RMSE = \sqrt{[\sum_{i = 1}^{n} (E i - M i) (E i - M i)] / n}

여기서, Ei : 모형에 의한 추정치 (estimated value)

Mi : 실측치 (observed value)

n : sample 수

(Eq. 7)

RRMSEM = (RMSE / STD of measured value)

(Eq. 8)

RRMSEE = (RMSE / STD of estimated value)

(Eq. 9)

RSTD = (STD of estimated value / STD of measured value)

이 경우 정확도 관점에서 RRMSEM와 RRMSEE의 두 가지 값이 모두 0.5 이하이면 그 모형이 ｢매우 적절함｣, 한 가지 값이라도 0.5 - 1.0이면 그 모형이 ｢적절함｣이라고 판정한다. 또한, 정밀도 관점에서 RSTD의 값이 1.0 이하이면 그 모형이 ｢매우 적절함｣ 또는 ｢적절함｣이라고 판정한다 (Liemohn et al., 2021). 정밀도 관점의 또 다른 기준인 Ta과 Ts 및 dT의 실측치 (M)에 대한 추정모형에 의한 추정치 (E)의 상관관계에 대한 상대정밀도 (relative sensitivity of estimation to measurement, RS [E/M]) 분석은 Eq. 10부터 Eq. 13까지의 과정을 통하여 분석하였으며, 이 경우 RS [E/M]) 값이 클수록 정밀도가 높다 (｢매우 적절함｣ 또는 ｢적절함｣)고 판정한다 (Goodman, 1960; Irsyard al et al., 2019).

(Eq. 10)

E = a \cdot M

(Eq. 11)

RS [E / M] = [(dE / dM) / (S_{E} / S_{M})]

(Eq. 12)

(SE / SM) = (a^{2} / R^{2})

(Eq. 13)

RS [E / M] = a / (a^{2} / R^{2}) = (R^{2} / a)

여기서, SE : E의 표준오차 (standard error)

SM : M의 표준오차 (standard error)

R2 : M에 대한 E의 직선 회귀 식에 대한 결정계수

Results and Discussion

가을배추 재배 기간의 기온과 토양온도 변화양상 및 시계열 변화 추정모형 설정

가을배추 재배 기간에 대한 Ta, Ts 및 dT의 경시적 변화양상을 볼 때 (Fig. 1 및 Table 1), Ta 및 Ts는 하루 또는 이틀 간격으로 오르락내리락 하지만 전체 경향은 온도가 계속 낮아졌으며, dT는 하루 또는 이틀 간격으로 오르락내리락 하지만 전체 경향은 온도가 증가 또는 감소 등 일정한 경향을 보이지 않았다. Ta 및 Ts의 최고 온도와 평균 온도는 각각 35.30 및 27.70°C와 19.89 및 17.32°C로서 Ts가 Ta보다 낮았으나, 최저온도는 각각 5.03 및 10.10°C로서 Ts가 Ta보다 높았다.

https://cdn.apub.kr/journalsite/sites/ksssf/2023-056-04/N0230560412/images/ksssf_2023_564_419_F1.jpg

Fig. 1.

Changes in air temperature (Ta: left), soil temperature (Ts: middle) and the difference (dT: right) according to Julian date.

Table 1.

The statistics of air temperature (Ta), soil temperature (Ts) and the difference (dT = Ta - Ts) at 15 cm soil depth during napa cabbage cultivation in autumn.

Statistics	Air temperature (Ta) (°C)	Soil temperature (Ts) (°C)	The difference (dT = Ta - Ts) (°C)
Maximum temperature	35.30	27.70	7.60
Average temperature	19.89	17.32	2.58
Minimum temperature	5.03	10.10	-6.67
Range	30.27	17.60	14.27
Standard deviation	6.02	4.90	3.51
Standard error	0.771	0.627	0.450

또한, Ta 및 Ts의 시계열 변화에 대하여 온도의 변화양상이 계속 낮아지는 기간이므로 독립 구간이라는 관점에서 그 추정모형을 각각 Eq. 14 및 Eq. 15와 같이 로그 (ln) 함수 형태인 (LMTa 및 LMTs)로 선정하고 최소제곱법에 따라 오차가 최소인 계수를 산정하여 모형을 설정하였다 (Fig. 2). LMTa 및 LMTs 모형의 계수 a 값 (Eq. 14 및 Eq. 15)을 볼 때, Ta 및 Ts 각각 -82.45 및 -74.34이었다. 이는 시간이 경과 함에 따라 온도가 낮아지는 정도는 Ta가 Ts 보다 더 컸다는 것을 의미한다.

(Eq. 14)

LMTa : Ta = - 82.45 \cdot \ln (JD) + 487.23

(Eq. 15)

LMTs : Ts = - 74.34 \cdot \ln (JD) + 438.72

여기서, JD : Julian date

https://cdn.apub.kr/journalsite/sites/ksssf/2023-056-04/N0230560412/images/ksssf_2023_564_419_F2.jpg

Fig. 2.

Estimation models for air (linear model for Ta, LMTa: left) and soil temperature (linear model for Ts, LMTs: right).

LMTa 및 LMTs 모형 검증결과, 정확성 관점에서 볼 때, LMTa 및 LMTs의 RMSE는 각각 3.242 및 1.732이었으며, RRMSEM과 RRMSEE는 각각 0.539와 0.637 및 0.288과 0.378이었다 (Table 2). 이를 기준으로 하여 LMTa는 ｢적절함｣으로, LMTs는 ｢매우 적절함｣으로 판정되었다. 상호관련성 관점에서 볼 때, R²값은 LMTa 및 LMTs 각각 0.715 및 0.877로서 모두 통계적으로 고도의 유의성이 인정되어 모두 ｢매우 적절함｣으로 판정되었다 (Table 2). 정밀도 관점에서 볼 때, LMTa 및 LMTs의 RSTD는 각각 0.845 및 0.762로서 모두 0.5 - 1.0이었으며, RS [E/M]는 각각 0.626 및 0.867로서 (Table 3 및 Fig. 3) LMTa는 ｢적절함｣으로, LMTs는 ｢매우 적절함｣으로 판정되었다. 이와 같은 결과에 따라 종합적으로 볼 때, LMTa는 ｢적절함｣으로, LMTs는 ｢매우 적절함｣으로 판단되었다.

Table 2.

The parameters and indices of measured (M) and estimated value (E) to verify the accuracy and association of the LMTa (linear model for Ta) and LMTs (linear model for Ts) for air (Ta) and soil temperature (Ts), respectively.

LMTa				LMTs
Parameter	Value	Index	Value	Parameter	Value	Index	Value
∑(M-E)²	971.5	RMSE	3.242	∑(M-E)²	206.8	RMSE	1.732
N	61	RRMSEM	0.539	N	61	RRMSEM	0.288
STD (M)	6.018	RRMSEE	0.637	STD (M)	4.898	RRMSEE	0.378
STD (E)	4.475	R²	0.715	STD (E)	4.533	R²	0.877

Table 3.

The parameters and indices of measured (M) and estimated value (E) to verify the precision of the LMTa (linear model for Ta) and LMTs (linear model for Ts) for air (Ta) and soil temperature (Ts), respectively.

LMTa				LMTs
Parameter	Value	Index	Value	Parameter	Value	Index	Value
STD (M)	6.018	RSTD [E/M]	0.845	STD (M)	4.898	RSTD [E/M]	0.762
STD (E)	4.475			STD (E)	4.533
R²	0.611			R²	0.861
a	0.976	RS [E/M]	0.626	a	0.992	RS [E/M]	0.867

https://cdn.apub.kr/journalsite/sites/ksssf/2023-056-04/N0230560412/images/ksssf_2023_564_419_F3.jpg

Fig. 3.

Relationship between measured and estimated value by the LMTa (linear model for Ta) and LMTs (linear model for Ts) for air temperature (left) and soil temperature (right), respectively.

기온에 대한 토양온도 및 온도 차이 추정모형 설정

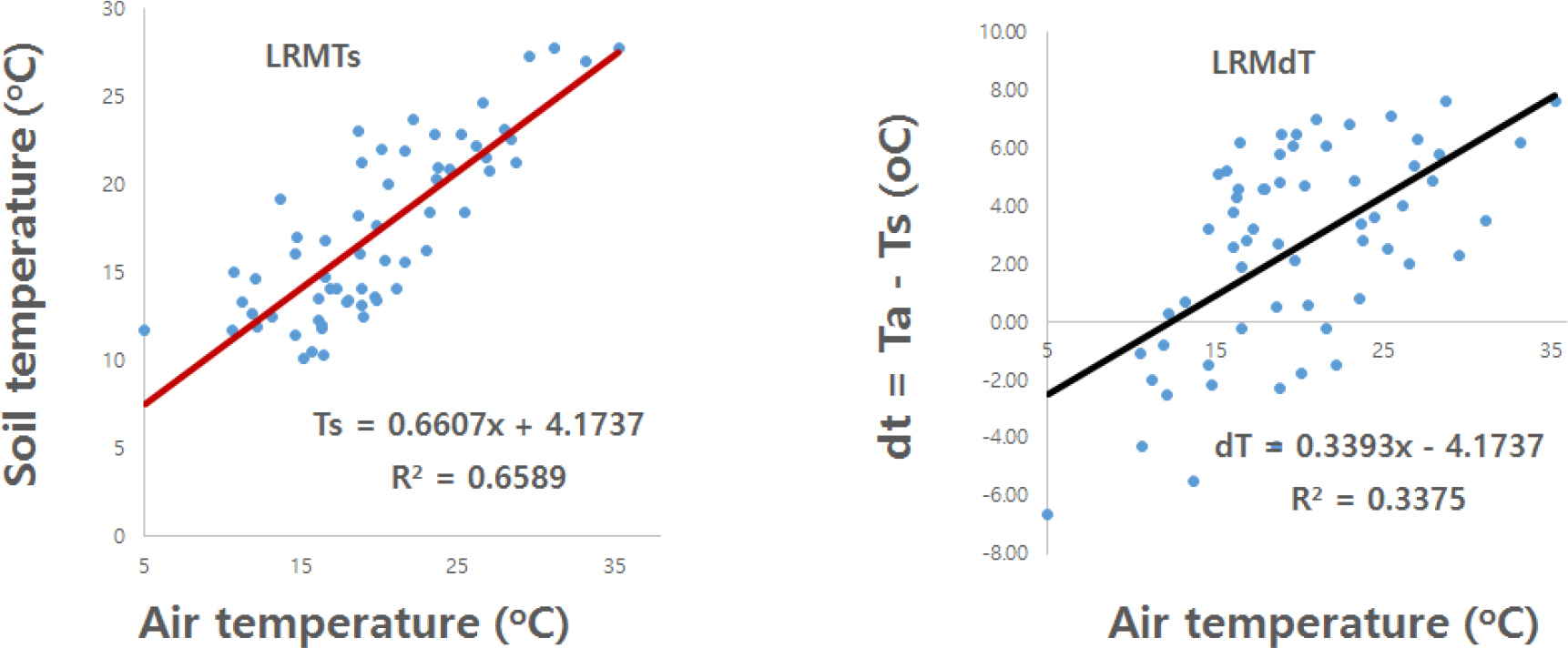
Ta 변화에 따른 Ts 및 dT의 변화 추정모형을 각각 Ta에 대한 직선 회귀 식인 일차함수인 LRMTs 및 LRMdT로 선정하고 최소제곱법에 따라 오차가 최소인 계수를 산정하여 모형을 설정하였으며 (Fig. 4), LRMTs 및 LRMdT의 경우 각각 Eq. 16 및 Eq. 17과 같다. Ta가 높을수록 Ts도 높았다. 이와 같은 결과는 Ta가 Ts 변화에 영향을 미치는 가장 중요한 인자라는 연구 (Park et al., 2014; Grosse et al., 2016) 결과 및 Ta과 Ts는 깊은 상관관계가 있다는 연구 (Kang et al., 2000) 결과와 유사한 결과를 나타내었다. 또한, 이와 같은 결과는 Ta가 높을수록 태양열이라는 수열 인자 (input parameter of heat)의 영향으로 Ta와 Ts는 정비례 관계를 나타내었다고 사료 된다. 또한, Ta가 높을수록 dT도 높았다. 이와 같은 결과는 본 연구의 시험 시기가 온도가 계속 낮아지는 시기이었고, Ta와 Ts 변화양상은 정비례 관계이었으며, 온도가 낮아지는 정도는 Ta가 Ts 보다 더 컸든 (Eq. 14 및 Eq. 15) 것에 기인 되었다고 사료 된다.

(Eq. 16)

LRMTs : Ts = 0.6607 \cdot Ta + 4.1737

(Eq. 17)

LRMdT : dT = 0.3393 \cdot Ta + 4.1737

https://cdn.apub.kr/journalsite/sites/ksssf/2023-056-04/N0230560412/images/ksssf_2023_564_419_F4.jpg

Fig. 4.

Estimation models for soil temperature (linear regression model for Ts, LRMTs: left) and the difference (linear regression model for dT, LRMdT: right).

LRMTs 및 LRMdT 모형 검증결과, 정확성 관점에서 볼 때, LRMTs 및 LRMdT의 RMSE는 공히 2.885이었으며, RRMSEM과 RRMSEE는 각각 0.589와 0.726 및 0.821과 1.413이었다 (Table 4). 이를 기준으로 하여 LRMTs는 0.5 - 1.0 이하로서 ｢적절함｣으로 판정되나, LRMdT는 1.0 이상으로서 ｢적절하지 않음｣으로 판정되었다. 상호관련성 관점에서 볼 때, LRMTs의 R²값은 0.659로서 통계적으로 유의성이 인정되어 ｢적절함｣으로 판정되었으며, LRMdT의 R²값은 0.338로서 비록 통계적으로 유의성은 인정되었으나 그 값이 너무 낮기에 ｢적절하지 않음｣으로 판정되었다. 정밀도 관점에서 볼 때, LRMTs 및 LRMdT의 RSTD는 각각 0.812 및 0.581이었으며, RS [E/M]은 각각 0.508 및 0.213 (Table 5 및 Fig. 5)으로서 LRMTs는 ｢적절함｣으로 판정되었으나, LRMdT는 ｢적절하지 않음｣으로 판정되었다. 이와 같은 결과에 따라 종합적으로 볼 때, LRMTs는 ｢적절함｣으로 판정되나, LRMdT는 ｢적절하지 않음｣으로 판단되었다.

Table 4.

The parameters and indices of measured (M) and estimated value (E) to verify the accuracy and association of the LRMTs (linear regression model for Ts) and the LRMdT (linear regression model for dT) for soil temperature (Ts) and the difference (dT = Ta - Ts), respectively.

LRMTs				LRMdT
Parameter	Value	Index	Value	Parameter	Value	Index	Value
∑(M-E)²	491.0	RMSE	2.885	∑(M-E)²	491.0	RMSE	2.885
N	61	RRMSEM	0.589	N	61	RRMSEM	0.821
STD (M)	4.898	RRMSEE	0.726	STD (M)	3.515	RRMSEE	1.413
STD (E)	3.976	R²	0.659	STD (E)	2.042	R²	0.338

Table 5.

The parameters and indices of measured (M) and estimated value (E) to verify the precision of the LRMTs (linear regression model for Ts) and the LRMdT (linear regression model for dT) for soil temperature (Ts) and the difference (dT = Ta - Ts), respectively.

LRMTs				LRMdT
Parameter	Value	Index	Value	Parameter	Value	Index	Value
STD (M)	4.898	RSTD [E/M]	0.812	STD (M)	3.515	RSTD [E/M]	0.581
STD (E)	3.976			STD (E)	2.042
R²	0.495			R²	0.122
a	0.975	RS [E/M]	0.508	a	0.572	RS [E/M]	0.213

https://cdn.apub.kr/journalsite/sites/ksssf/2023-056-04/N0230560412/images/ksssf_2023_564_419_F5.jpg

Fig. 5.

Relationship between measured and estimated value by the LRMTs (linear regression model for Ts) for soil temperature (Ts: left) and LRMdT (linear regression model for dT) for the difference (dT = Ta - Ts: right), respectively.

기온과 토양수분 함량에 의한 온도 차이 추정모형 설정

Ta과 Qv 두 개의 독립변수를 채택한 이중 회귀 식을 dT의 추정모형 (DRMdT)으로 선정하고 최소제곱법에 따라 오차가 최소인 계수를 산정하여 모형을 설정한 결과 Eq. 18과 같다. 즉, Ta가 높을수록 또 Qv가 낮을수록 dT는 높은 상관관계를 보였다. 이와 같은 결과는, 이중 회귀 식에서 종속 변수와 독립변수의 상호 직접적인 인과관계라고 해석할 수는 없으나, 태양열이라는 수열 인자의 영향으로 Ta과 Ts는 정비례 관계에 있으며, Qv가 낮을수록 Qv가 높은 경우보다, 열전도도가 낮고 또한, 본 연구의 시험 시기가 온도가 계속 낮아지는 시기이었기에 상대적으로 비열이 낮아 열 방사율이 더 크기 때문에 (Lal and Shukla, 2004) Ts의 낮아지는 정도가 더 빠른 것에 기인 되었다고 사료 된다.

(Eq. 18)

DRMdT : dT = 9.4036 + 0.7127 \cdot Ta - 0.8875 \cdot Qv

DRMdT의 검증결과, 정확성 관점에서 볼 때, RMSE는 1.907이었으며, RRMSEM 및 RRMSEE는 각각 0.543 및 0.644로서 0.5 - 1.0이었다 (Table 6). 이를 기준으로 하여 ｢적절함｣으로 판정되었다. 상호관련성 관점에서 볼 때, R²값은 0.711로서 통계적으로 고도의 유의성이 인정되어 ｢매우 적절함｣으로 판정되었다. 정밀도 관점에서 볼 때, RSTD는 0.847이었으며 RS [E/M]는 0.823 (Fig. 6 및 Table 7)으로서 ｢매우 적절함｣으로 판정되었다. 이와 같은 결과에 따라 종합적으로 볼 때, DRMdT는 ｢매우 적절함｣으로 판단되었다.

Table 6.

The parameters and indices of measured (M) and estimated value (E) to verify the accuracy and association of the DRMdT (double regression model for dT) for the difference (dT = Ta - Ts).

Parameter	Value	Index	Value
∑(M-E)²	214.5	RMSE	1.907
N	61	RRMSEM	0.543
STD (M)	3.515	RRMSEE	0.644
STD (E)	2.963	R²	0.711

https://cdn.apub.kr/journalsite/sites/ksssf/2023-056-04/N0230560412/images/ksssf_2023_564_419_F6.jpg

Fig. 6.

Relationship between measured and estimated value by the DRMdT (double regression model for dT) for the difference (dT = Ta - Ts).

Table 7.

The parameters and indices of measured (M) and estimated value (E) to verify the precision of the DRMdT (double regression model for dT) for the difference (dT = Ta - Ts).

Parameter	Value	Index	Value
STD (M)	3.515	RSTD [E/M]	0.847
STD (E)	2.963
R²	0.669
a	0.813	RS [E/M]	0.823

Conclusions

본 연구는 전북 완주에 소재한 농촌진흥청 국립원예특작과학원의 사양토 시험 포장에 가을배추를 재배하면서, 2022년 9월 16일부터 2022년 11월 16일까지 매일 10:00에 측정된 기온 (Ta), 토양온도 (Ts), 온도 차이 (dT = Ta - Ts) 및 토양수분 함량 (Qv)을 분석하여 구명한 결과는 다음과 같다.

Ta의 시계열에 대한 추정모형인 LMTa는 ｢적절함｣으로 판단되었으며, Ts의 시계열에 대한 추정모형인 LMTs는 ｢매우 적절함｣으로 판단되었다. Ta에 대한 Ts의 추정모형인 LRMTs는 ｢적절함｣으로 판단되었으며, Ta과 Qv 두 개의 독립변수를 채택한 이중 회귀 식의 dT 추정모형인 DRMdT는 ｢매우 적절함｣으로 판단되었다.

Acknowledgements

본 연구는 농촌진흥청 연구사업 (공동과제명: 배추 고추의 토양수분 이동 특성 및 최적 간단 관개 방법 구명, 공동과제 번호: PJ017049)의 지원에 의해 수행되었습니다.

References

Chakraborty, P.K., S. Banerjee, R. Nath, and S. Samanta. 2021. Assessing congenial soil temperature and its impact on root growth, grain yield of summer rice under varying water stress condition in Lower Gangetic Plain of India. J. Saudi Soc. Agric. Sci. 21(2):98-107. 10.1016/j.jssas.2021.07.001

Chi, Y., J. Sun, Y. Sun, S. Liu, and Z. Fu. 2020. Multi-temporal characterization of land surface temperature and its relationships with normalized difference vegetation index and soil moisture content in the Yellow River Delta, China. Global Ecol. Conserv. 23:e01092. 10.1016/j.gecco.2020.e01092

Delage, P. 2013. On the thermal impact on the excavation damaged zone around deep radioactive waste disposal. J. Rock Mech. Geotech. Eng. 5(3):179-190. 10.1016/j.jrmge.2013.04.002

Derradji, M. and M. Aiche. 2014. Modeling the soil surface temperature for natural cooling of buildings in hot climates. Proc. Comput. Sci. 32(2014):615-621. 10.1016/j.procs.2014.05.468

Eom, K.C., E.R. Son, and K.S. Ryu. 1990. Changes in evapotranspiration and soil water status to vinyl mulching. Korean J. Soil Sci. Fert. 23(2):100-106.

Ferreira, L.S. and D.H.S. Duarte. 2019. Exploring the relationship between urban form, land surface temperature and vegetation indices in a subtropical megacity. Urban Clim. 27:105-123. 10.1016/j.uclim.2018.11.002

Fu, X.l., Z.B. Yu, Y.J. Ding, Y. Tang, H.S. Lu, X.I. Jiang, and Q. Ju. 2018. Analysis of influence of observation operator on sequential data assimilation through soil temperature simulation with common land model. Water Sci. Eng. 11(3):196-204. 10.1016/j.wse.2018.09.003

Garcia, L.M., N.M. Pinyol, A. Lloret, and E.A. Soncco. 2023. Influence of temperature on residual strength of clayey soils. Eng. Geol. 323:107220. 10.1016/j.enggeo.2023.107220

Goodman, L.A. 1960. On the exact variance of products. J. Am. Stat. Assoc. 55:708-713. 10.1080/01621459.1960.10483369

Grosse, G., S. Goetz, A.D. McGuire, V.E. Romanovsky, and E.A.G. Schuur. 2016. Changing permafrost in a warming world and feedbacks to the Earth system. Environ. Res. Lett. 11(4):040201. 10.1088/1748-9326/11/4/040201

Hashemi, A., M. Sutman, and H. Abuel-Naga. 2022. Thermomechanical response of kaolin clay-concrete interface in the context of energy geostructures. Can. Geotech. J. 60(3):380-396. 10.1139/cgj-2022-0172

Irsyard al, M.I., A. Halog, and R. Nepal. 2019. Renewable energy for climate change mitigation: An analysis of uncertanity and errors. Renewable Energy 130:536-546. 10.1016/j.renene.2018.06.082

Islam, M.A., R. Lubbad, S.A.G. Amiri, V. Isaev, Y. Shevchuk, A.V. Uvarova, M.S. Afzal, and A. Kumar. 2021. Modeling the seasonal variations of soil temperatures in the Arctic coasts. Polar Sci. 30:100732. 10.1016/j.polar.2021.100732

Kang, S., S. Kim, S. Oh, and D. Lee. 2000. Predicting spatial and temporal patterns of soil temperature based on topography surface cover and air temperature. For. Ecol. Manage. 136(1-3):173-184. 10.1016/S0378-1127(99)00290-X

Kim, M., W.K. Lee, K. Nam, H. Yu, S.E. Choi, and C.G. Kim. 2014. Estimating stand volume Pinus densiflora forest based on climate change scenario in Korea. J. Korean For. Soc. 103(1):105-112. 10.14578/jkfs.2014.103.1.105

Krause, P., D.P. Boyle, and F. Base. 2005. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 5:89-97. 10.5194/adgeo-5-89-2005

Lal, R. and M.K. Shukla. 2004. Principles of soil physics: Soil temperature and heat flow in soil. p. 515-555. Marcel Dekker, Inc., New York ‧ Basel, USA. 10.4324/9780203021231

Legates, D.R. and G.L.Jr. Mc Cabe. 1999. Evaluating the use of "goodness-of-fit" measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 35(1):233-241. 10.1029/1998WR900018

Li, X., Y. Zhou, G.R. Asrar, and Z. Zhu. 2018. Creating a seamless 1 km resolution daily land surface temperature data set for urban and surrounding area in the conterminous United States. Remote Sens. Environ. 206:84-97. 10.1016/j.rse.2017.12.010

Liemohn, M.W., A.D. Shane, A.R. Azari, A.K. Petersen, B.M. Swiger, and A. Mukhopadhyay. 2021. RMSE is not enough: Guidelines to robust data-model comparisons for magnetospheric physics. J. Atmos. Sol.-Terr. Phys. 218:105624. 10.1016/j.jastp.2021.105624

Lloyd, J. and J.A. Taylor. 1994. On the temperature dependence of soil respiration. Funct. Ecol. 8(3):315-323. 10.2307/2389824

Mandel, J. 1964. The statistical analysis of experimental data. p. 58-77, 363-389. John Wiley & Sons, New York, USA.

Moriasi, D.N., J.G. Armold, M.W. Van Liew, R.L. Bingner, R.D. Harmel, and T.L. Veith. 2007. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 50(3):885-900. 10.13031/2013.23153

Muro, J., A. Strauch, S. Heinamann, S. Steinbach, F. Thonfeld, B. Waske, and B. Diekkruger. 2018. Land surface temperature trends as indicator of land use changes in wetlands. Int. J. Appl. Earth Obs. Geoinf. 70:62-71. 10.1016/j.jag.2018.02.002

Naseri, F., M. Azari, and M.T. Dastorani. 2021. Spatial optimization of soil and water conservation practices using coupled SWAT model and evoluyionary algorithm. Int. Soil Water Conserv. Res. 9(4):566-577. 10.1016/j.iswcr.2021.04.002

Nash, J.E. and J.V. Sutcliffe. 1970. River flow forecasting through conceptual models part I - A discussion of principles. J. Hydrol. 10(3):282-290. 10.1016/0022-1694(70)90255-6

Ning, S., J. Song, J. Ru, Z. Zhou, J. Zhang, X. Liu, Y. Hui, Y. Ma, and S.,Wan. 2020. Nonadditive and legacy effects of spring and autumn warming on soil respiration in an old-field grassland. Ecosystems 24(2):421-433. 10.1007/s10021-020-00525-4

Park, H., A.B. Sherstiukov, A.N. Fedorov, I.V. Polyakov, and J.E. Walsh. 2014. An observation based assessment of the influences of air temperature and snow depth on soil temperature in Russia. Environ. Res. Lett. 9(6):064026. 10.1088/1748-9326/9/6/064026

Pham, T.A. and M. Sutman. 2023. A simplified method for bearing capacity analysis of energy piles integrating temperature-dependent model of soil-water characteristic curve. J. Geotech. Geoenviron. Eng. 149(9):1-23. 10.1061/JGGEFK.GTENG-11095

Pham, T.A., A. Hashemi, M. Sutman, and G.M. Medero. 2023. Effect of temperature on the soil water retention characteristics in unsaturated soils: Analytical and experimental approaches. Soils Found. 63:101301. 10.1016/j.sandf.2023.101301

Shein, E.V., A.V. Dembovetsky, and S.S. Panina. 2013. Modeling soil water movement under low head ponding and gravity infiltration using data determined with different methods. Proc. Environ. Sci. 19(2013):553-557. 10.1016/j.proenv.2013.06.062

Smith, S.L., V.E. Romanovsky, A.G. Lewkowicz, C.R. Burn, M. Allard, G.D. Clow, K. Yoshikawa, and J. Throop. 2010. Thermal state of permafrost in North America: A contribution to the international polar year. Permafrost Periglacial Processes 21(2):117-135. 10.1002/ppp.690

Thota, S.K. and F. Vahedifard. 2021. Stability analysis of unsaturated slopes under elevated temperatures. Eng. Geol. 293:106317. 10.1016/j.enggeo.2021.106317

Urqueta, H., J. Jodal, C. Herrera, H.G. Wilke, A. Medina, J. Urrutia, E. Custodio, and J. Rodriguez. 2018. Land surface temperature as an indicator of the unsaturated zone thickness: A remote sensing approach in the Atacama Desert. Sci. Total Environ. 612:1234-1248. 10.1016/j.scitotenv.2017.08.30528892867

Wang, X.C. and J. Li. 2010. Evaluation of crop yield and soil water estimates using the epic model for the loess plateau of China. Math. Comput. Modell. 51(2010):1390-1397. 10.1016/j.mcm.2009.10.030

Watson, J. and A. Challinor. 2013. The relative importance of rainfall, temperature and yield data for a regional-scale crop model. Agric. For. Meteorol. 170:47-57. 10.1016/j.agrformet.2012.08.001

Zhang, T., J.C. Huang, Q. Lei, X. Liang, S. Lindsey, J. Luo, A.X. Zhu, W. Bao, and H. Liu. 2021. Catena 208:105696. 10.1016/j.catena.2021.105696

Korean Journal of Soil Science and Fertilizer 한국토양비료학회 학회지 ISSN:0367-6315(Print) 2288-2162(Online)

Preview

Numerical Approach for Air Temperature, Soil Temperature and the Difference between Them with Julian Date under Napa Cabbage

ABSTRACT

Relationship between measured and estimated value by the DRMdT (double regression model for dT) for the difference (dT = Ta - Ts).

MAIN

(Eq. 1)

(Eq. 2)

(Eq. 3)

(Eq. 4)

(Eq. 5)

(Eq. 6)

(Eq. 7)

(Eq. 8)

(Eq. 9)

(Eq. 10)

(Eq. 11)

(Eq. 12)

(Eq. 13)

Fig. 1.

Changes in air temperature (Ta: left), soil temperature (Ts: middle) and the difference (dT: right) according to Julian date.

Table 1.

The statistics of air temperature (Ta), soil temperature (Ts) and the difference (dT = Ta - Ts) at 15 cm soil depth during napa cabbage cultivation in autumn.

(Eq. 14)

(Eq. 15)

Fig. 2.

Estimation models for air (linear model for Ta, LMTa: left) and soil temperature (linear model for Ts, LMTs: right).

Table 2.

The parameters and indices of measured (M) and estimated value (E) to verify the accuracy and association of the LMTa (linear model for Ta) and LMTs (linear model for Ts) for air (Ta) and soil temperature (Ts), respectively.

Table 3.

The parameters and indices of measured (M) and estimated value (E) to verify the precision of the LMTa (linear model for Ta) and LMTs (linear model for Ts) for air (Ta) and soil temperature (Ts), respectively.

Fig. 3.

Relationship between measured and estimated value by the LMTa (linear model for Ta) and LMTs (linear model for Ts) for air temperature (left) and soil temperature (right), respectively.

(Eq. 16)

(Eq. 17)

Fig. 4.

Estimation models for soil temperature (linear regression model for Ts, LRMTs: left) and the difference (linear regression model for dT, LRMdT: right).

Table 4.

The parameters and indices of measured (M) and estimated value (E) to verify the accuracy and association of the LRMTs (linear regression model for Ts) and the LRMdT (linear regression model for dT) for soil temperature (Ts) and the difference (dT = Ta - Ts), respectively.

Table 5.

The parameters and indices of measured (M) and estimated value (E) to verify the precision of the LRMTs (linear regression model for Ts) and the LRMdT (linear regression model for dT) for soil temperature (Ts) and the difference (dT = Ta - Ts), respectively.

Fig. 5.

Relationship between measured and estimated value by the LRMTs (linear regression model for Ts) for soil temperature (Ts: left) and LRMdT (linear regression model for dT) for the difference (dT = Ta - Ts: right), respectively.

(Eq. 18)

Table 6.

The parameters and indices of measured (M) and estimated value (E) to verify the accuracy and association of the DRMdT (double regression model for dT) for the difference (dT = Ta - Ts).

Fig. 6.

Relationship between measured and estimated value by the DRMdT (double regression model for dT) for the difference (dT = Ta - Ts).

Table 7.

The parameters and indices of measured (M) and estimated value (E) to verify the precision of the DRMdT (double regression model for dT) for the difference (dT = Ta - Ts).

Acknowledgements

References