Introduction
작물 재배에서 관개량을 결정하거나 농업용수를 효율적으로 관리하기 위해서는 기본증발산량과 작물계수 등의 자료가 기본적으로 필요하다 (Nam et al., 2017; Lee et al., 2018). 기본증발산량은 잔디 등 기준작물이 수분 스트레스를 받지 않는 조건에서의 증발산량이다. 중량 라이시미터 등 장비를 이용한 기본증발산량의 실측은 비용 등의 이유로 조밀한 관측망을 구성하기에는 현실적으로 매우 어렵다. 따라서 기본증발산량과 밀접한 관련이 있는 기상자료를 이용하여 이론적인 방법으로 기본증발산량을 산정하는 것이 일반적이다. 약 50여 가지의 방법들 가운데 FAO Penman-Monteith 공식 (Allen et al., 1998)을 세계적으로 가장 많이 사용하여 왔다. Jensen et al. (1990)은 20가지의 기본증발산량 공식 가운데 건조지역과 습윤지역 모두 FAO Penman-Monteith 공식이 가장 우수하다고 하였으며, Cai et al. (2007)과 Pereira et al. (2015)도 FAO Penman-Monteith 공식의 우수성을 보고하였고, 세계적으로 많은 연구자들이 이 공식을 이용하여 왔다.
그런데 FAO Penman-Monteith 공식으로 기본증발산량을 추정하려면 일사량, 기온, 상대습도, 풍속 등 기상자료가 필요하다. 이들 기상자료를 모두 관측하는 기상관측소는 매우 제한적이며, 미래 기후변화 시나리오에서도 이들 자료를 모두 제공하지 않고 있다. 따라서 기상자료가 부족하거나 결측된 지역이나 여건에서 사용할 수 있도록 온도나 복사열 자료 등 기본적인 기상 정보만으로도 기본증발산량을 산정할 수 있는 공식들이 개발되어 사용되어져 왔다. 이들 가운데 Hargreaves 공식 (Hargreaves and Samani, 1985)은 온도 자료만 있으면 기본증발산량을 추정할 수 있어 단순하고 계산이 간단하면서도 비교적 정확하다. 그래서 FAO는 온도 자료만 있을 경우에는 이 공식을 활용하여 기본증발산량을 추정하도록 제안하였다 (Allen et al., 1998). 특히 우리나라를 포함한 온대 지역에서는 증발산량의 80% 정도를 온도와 태양 복사열로 설명이 가능하므로 (Vanderlindes et al., 2004), 많은 연구자들이 Hargreaves 공식을 활용하여 기본증발산량을 추정하고 있다.
Hargreaves 공식을 활용하는 데 있어서, 풍속이 3 m s-1 이상인 지역에서는 기본증발산량을 과소평가하고, 상대습도가 높으면 과대평가하는 경향이 있다 (Allen et al., 1998; Cordova et al., 2015; Kim et al., 2017)는 점을 유의해야 한다. 또한 최고기온과 최저기온의 차이에 영향을 줄 수 있는 요인이 내륙 지역과 해안 지역이 서로 다르다 (Allen et al., 1998). Todorovic et al. (2013)는 지역에 따라 태양 복사량 등 기후 특성을 반영하여 계수를 조정하면 추정 정확도가 향상된다고 하였다. Kim et al. (2017)은 안동댐 유역 10지점에서 제한적인 기상자료 조건에서의 기본증발산량을 추정하였는데, Hargreaves 공식은 FAO Penman-Monteith 방법과 비교했을 때 과대 추정하는 경향을 보였으므로 지역 특성을 고려한 매개변수가 필요하다고 하였다. Yoon and Choi (2018)는 우리나라 11개 지점에서 30년 (1981-2010) 동안 측정된 기상자료와 Penman-Monteith 공식, Priestley-Taylor 공식, Hargreaves 공식을 이용하여 기상자료의 결측에 따른 기본증발산량의 민감도를 비교 분석한 결과, Hargreaves 공식은 경향성은 높지만 오차가 크므로 지역적 기후 특성을 고려하여 지역별 매개변수를 조정함으로써 정확도를 높일 필요가 있다고 하였다.
Lee and Park (2008)은 강원도 네 지점을 포함하여 우리나라 23개 지점에서 1997-2006년에 관측된 기상자료를 이용하여 Hargreaves 공식의 지역별 매개변수를 추정하였다. 또한 Moon et al. (2013)은 일사량과 기온과의 관계를 분석하여 이를 바탕으로 수정된 Hargreaves 공식을 제안하였으며, 이 수정 공식에서의 지역별 매개변수를 71지점에서 추정하였다. 즉 그들은 최고기온과 최저기온의 차이에 대한 지수를 0.50에서 0.58로 바꾼 다음에 계수를 조정하였는데, Allen et al. (1998)과 Todorovic et al. (2013) 등 여러 연구자들은 온도 차이의 지수는 0.50으로 그대로 둔 채로 지역별로 계수만 바꾸는 것을 제안하였다.
이 연구의 목적은 강원도 11지점에서 온도 차이의 지수는 바꾸지 않고 Hargreaves 계수만 보정하여 지역적 기후 특성을 반영함으로써 기본증발산량의 추정의 정확도를 높이는 데 있다. 이를 위하여 FAO Penman-Monteith 공식과 11지점의 최근 (2007-2017) 기상 자료로 산정된 기본증발산량을 기준으로 하여 Hargreaves 공식의 계수를 보정하였으며, 그 결과를 이 논문에서 보고하는 바이다.
Materials and Methods
FAO Penman-Monteith 방법을 이용한 기본증발산량 추정
강원도에서 기온, 상대습도, 풍속, 일조시간을 모두 측정하고 있는 11지점을 대상으로 하여, 2007년부터 2017년까지 11년 동안의 기상자료를 활용하여 FAO Penman-Monteith 공식 (Eq. 1)으로 기본증발산량을 추정하였다.
| $$ET_0=\frac{0.408\triangle(R_n-G)+\gamma{\displaystyle\frac{900}{T+273}}u_2(e_s-e_a)}{\triangle+\gamma\;(1+0.34u_2)}$$ | (Eq. 1) |
ET0는 기본증발산량 (mm d-1), Δ는 포화 수증기압과 온도 곡선의 기울기 (kPa °C-1), Rn은 이용 가능 복사열 (MJ m-2 d-1), G는 토양열 유동 밀도 (MJ m-2 d-1), γ는 건습계 상수 (kPa °C-1), T는 일 평균기온 (°C), u2는 지상 2 m 높이에서의 풍속 (m s-1), es와 ea는 각각 포화 수증기압(kPa)과 실제 수증기압(kPa)이다.
Hargreaves 공식을 이용한 기본증발산량 추정 및 계수 최적화
FAO Penman-Monteith 공식으로 기본증발산량을 추정한 같은 지점에서 같은 기간의 온도 자료를 가지고 Hargreaves 공식 (Eq. 2)으로 기본증발산량을 산정하였다.
| $$ET_0=K_{ET}R_a(T+17.8)\sqrt{(T_{max}-T_{min})}$$ | (Eq. 2) |
KET는 Hargreaves and Samani (1985)가 미국 캘리포니아주 데이비스에서의 8년간의 기상 자료를 이용하여 산정한 값으로 0.0023이 기본값이며, Ra는 대기권 밖에서의 복사에너지를 증발산량 단위 (mm d-1)로 환산한 값으로 위도와 줄리안데이로 계산할 수 있으며, Tmax와 Tmin은 각각 일 최고기온 (°C)과 일 최저기온 (°C)이다.
Hargreaves 공식의 계수의 최적화는 FAO Penman-Monteith 방법으로 추정한 기본증발산량을 기준으로 하여 Eq. 3과 마이크로소프트 엑셀의 해 찾기 기능을 이용하여 수행하였다.
| $$minimize(\sqrt{ET_{0PM}}-\sqrt{ET_{0H}})^2$$ | (Eq. 3) |
ET0PM는 FAO Penman-Monteith 공식을 이용하여 추정한 기본증발산량이며, ET0H는 Hargreaves 공식을 이용하여 추정한 기본증발산량이다.
Hargreaves 공식을 이용한 기본증발산량의 추정값을 FAO Penman-Monteith 방법에 따른 기본증발산량과 비교하기 위하여, root mean square error (RMSE)와 Nash-Sutcliffe coefficient of efficiency (NSC, Nash and Sutcliffe, 1970)를 각각 Eq. 4과 Eq. 5로 계산하였다.
| $$RMSE=\sqrt{\frac1n}\sum_{i=1}^n(ET_{0iH}-ET_{0iPM})^2$$ | (Eq. 4) |
| $$NSC=1-\frac{{\displaystyle\sum_{i=1}^n}(ET_{0iPM}-ET_{0iH})^2}{{\displaystyle\sum_{i=1}^n}(\overline{ET_{0iPM}}-ET_{0iH})^2}$$ | (Eq. 5) |
ET0iH는 Hargreaves 공식을 이용하여 계산한 i번째 기본증발산량이며, ET0iPM는 FAO Penman-Monteith 공식을 이용하여 계산한 i번째 기본증발산량, n은 자료의 개수, 는 FAO Penman-Monteith 공식을 이용하여 계산한 기본증발산량의 평균이다. RMSE는 오차의 크기를 나타내므로 0에 가까울수록 기준이 되는 값과 차이가 적고, NSC는 1에 가까울수록 정확도가 높음을 나타낸다.
Penman-Monteith-T 방법을 이용한 기본증발산량 추정
Allen et al. (1998)은 기온 자료만 있을 경우에 기본증발산량을 추정하는 방법으로 Hargreaves 공식의 이용과 더불어 다른 방법을 제안하였다. 즉, 태양 복사에너지는 최고기온과 최저기온의 차이를 이용하여 추정하고 (Eq. 6), 상대습도는 최저기온을 활용하여 추정하며 (Eq. 7), 풍속은 2 m s-1로 고정하여 기본증발산량을 계산하는 방법 (Penman-Monteith-T 방법)이다.
| $$R_s=k_{R_s}\sqrt{(T_{max}-T_{min})}R_a$$ | (Eq. 6) |
Rs는 지표면에 도달하는 태양 복사에너지 (MJ m-2 d-1)이며, kRs는 조정 계수(°C-0.5)로 내륙 지역에서는 0.16, 해안 지역에서는 0.19를 주로 쓰고 있다.
| $$e_a=e^0(T_{dew})=e^0(T_{min})=0.611exp\left(\frac{17.27T_{min}}{T_{min}+237.3}\right)$$ | (Eq. 7) |
e0(Tdew)와 e0(Tmin)는 각각 이슬점 온도와 일 최저기온에서의 포화 수증기압이다.
강원도 미래 기본증발산량 예측
강원지역에서 미래의 기본증발산량을 예측하기 위하여, 기상청에서 제공한 남한 상세 기후변화 시나리오의 Representative Concentration Pathways (RCP) 4.5와 RCP 8.5의 기온 자료와 이 연구에서 조정한 Hargreaves 계수를 이용하여 2040년, 2070년, 2100년의 기본증발산량을 추정하였다. 이 연구에서 이용한 기후변화 시나리오는 HadGEM3-RA (Atmospheric Regional Climate model of Hadley Centre Global Environment Model version 3) 지역기후 모델을 통해 생산되었다 (Kim et al., 2012).
Results and Discussion
Hargreaves 계수 보정 Hargreaves 공식에 따른 강원도 11지점의 기본증발산량 추정값이 FAO Penman-Monteith 방법의 기본증발산량과 차이가 최소가 되도록 Hargreaves 계수를 보정한 결과를 Table 1에 나타내었다. 춘천 등 내륙 영서지방은 0.00181-0.00199로 기본값인 0.0023보다 낮은 반면에, 강릉 등 해안 영동지방은 0.00275-0.00302로 기본값에 비해서 높았다.
Hargreaves 계수를 기본값인 0.0023으로 기본증발산량을 계산하였을 때와 Table 1의 보정값으로 계산하였을 때의 FAO Penman-Monteith 방법의 기본증발산량과 비교한 RMSE와 NSC를 Table 2에 제시하였다. Hargreaves 계수를 보정함으로써 오차의 크기를 나타내는 RMSE는 0.74-1.17 mm d-1에서 0.48-1.15 mm d-1로 낮아졌고, 추정 정확도를 나타내는 NSC는 0.56-0.77에서 0.56-0.90으로 높아졌다.
강원도 11지점에서 Hargreaves 계수를 보정하기 전과 후의 FAO Penman-Monteith 방법의 기본증발산량과의 산포도를 회귀식과 함께 Fig. 1에 나타내었다. 계수를 기본값인 0.0023으로 하였을 때에는 회귀식의 기울기가 내륙 영서지방은 1.12-1.22로 12-22% 과대 추정하는 경향을 보였으나, 계수를 보정하였을 때에는 0.95-0.98로 낮아져서 2-5% 과소 추정하였다. 한편 해안 영동지방은 계수를 보정하기 전에는 기울기가 0.79-0.88로 12-21% 과소 추정하였으나, 보정한 다음에는 0.93-0.94로 6-7% 과소 추정하는 것으로 줄었다.
Table 1. Modified Hargreaves coefficient for 11 regions in Gangwondo.
Table 2. Comparison between original and modified Hargreaves method in terms of RMSE and NSC compared with FAO Penman-Monteith reference evapotranspiration.
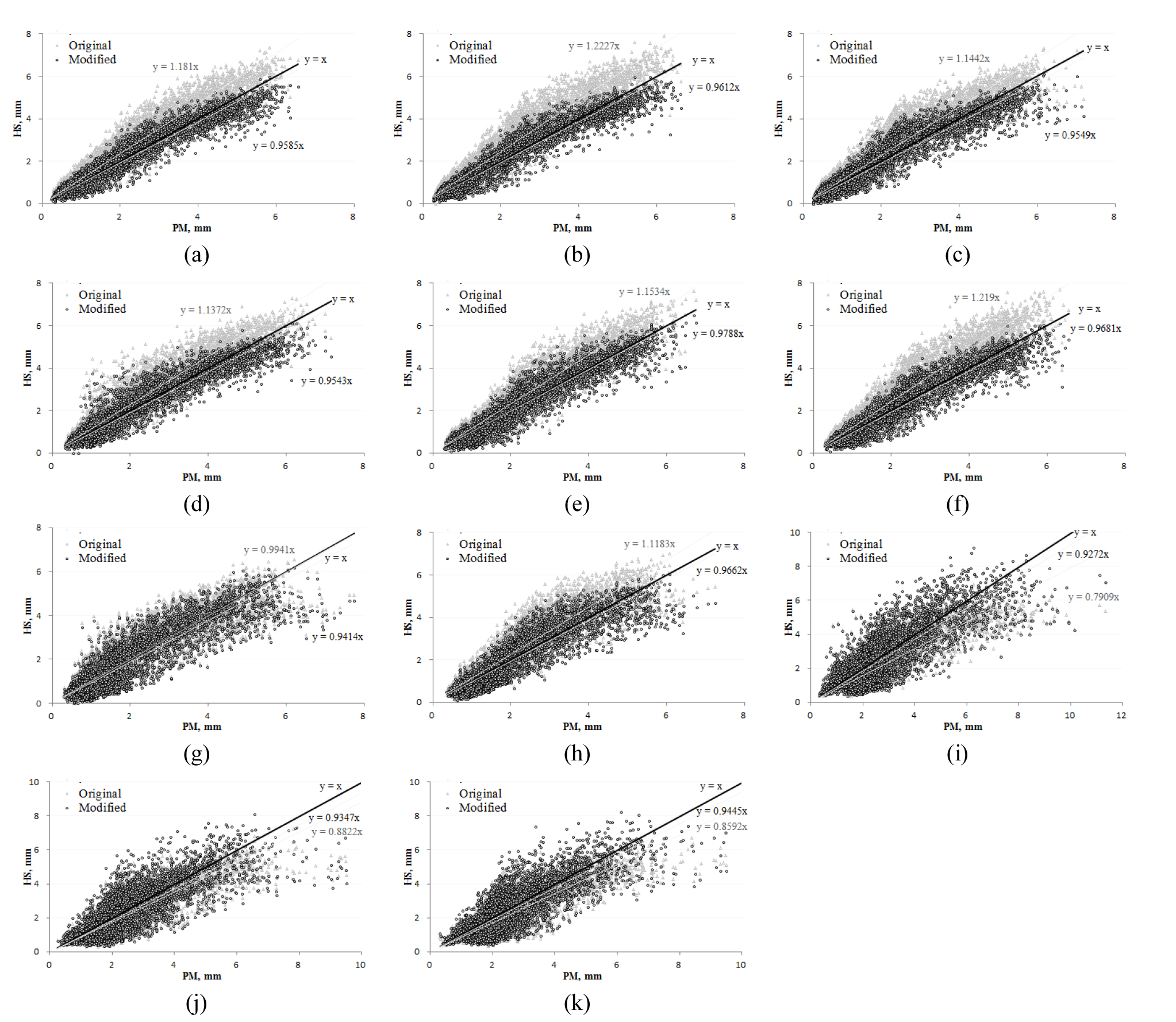
Fig. 1.
Comparison of original Hargreaves (gley triangle) versus modified Hargreaves (black circle) compared with Penman-Monteith reference evapotranspiration in (a) Chuncheon, (b) Hongcheon, (c) Cheorwon, (d) Wonju, (e) Inje, (f) Yeongwol, (g) Daegwallyeong, (h) Taebaek, (i) Gangneung, (j) Sokcho, and (k) Donghae.
Lee and Park (2008)이 1997-2006년에 관측된 기상자료를 바탕으로 조정한 춘천, 원주, 대관령, 강릉의 Hargreaves 계수를 이용하여 기본증발산량을 추정한 결과 RMSE는 0.59-1.23 mm d-1로 평균 0.84 mm d-1이었고, NSC는 0.51-0.85로 평균 0.71이었다 (Table 3). 이 논문에서 조정한 계수로 위의 네 지점을 추정하였을 때에는 RMSE는 0.48-1.15 mm d-1로 평균 0.73 mm d-1이었고, NSC는 0.57-0.90으로 평균 0.78이었다. 따라서 2007-2017년의 기상자료를 활용한 이 연구의 결과는 Lee and Park (2008)의 결과보다는 FAO Penman-Monteith 방법과 오차가 적고 정확도가 높은 것으로 판단된다.
Moon et al. (2013)이 Hargreaves 공식을 수정한 다음에 조정한 계수로 기본증발산량을 추정하였을 때에는 RMSE는 0.49-1.11 mm d-1로 평균 0.68 mm d-1이었고, NSC는 0.63-0.90으로 평균 0.79로, 이 연구의 결과와 비슷하였다 (Table 3). 내륙 영서지방은 이 연구의 결과가 더 우수하였지만, 해안 영동지방은 Moon et al. (2013)의 결과가 비교적 우수하였다.
Table 3. RMSE and NSC for method of Lee and Park (2008) and Moon et al. (2013) compared with FAO Penman-Monteith reference evapotranspiration.
Penman-Monteith-T 방법과의 비교
Penman-Monteith-T 방법 (Allen et al., 1998)에 따라 기본증발산량을 계산하였을 때의 RMSE는 0.65-1.13 mm d-1로 평균 0.77 mm d-1이었고, NSC는 0.59-0.83으로 평균 0.74이었다 (Table 4). Todorovic et al. (2013)과 Raziei and Pereira (2013)는 강수량이 기본증발산량보다 많은 습윤한 지역에서는 Penman-Monteith-T 방법을 이용하면 Hargreaves 방법에 비해서 과대 추정 정도가 낮아진다고 하였다. 이 연구에서도 Hargreaves 방법의 RMSE와 NSC는 각각 0.84 mm d-1와 0.69로 Penman-Monteith-T 방법에 비해 오차가 크고 정확도가 떨어졌는데, Hargreaves 계수를 조정하여 추정하였을 때에는 RMSE와 NSC는 각각 0.69 mm d-1와 0.78로 Penman-Monteith-T 방법에 비해서는 오차가 적고 정확도가 높았다.
Todorovic et al. (2013)은 강수량이 기본증발산량보다 많은 습윤한 지역에서 Penman-Monteith-T 방법을 이용하여 기본증발산량을 추정할 때에는 이슬점 온도를 평균 기온에서 1°C 낮게 하여 (Lawrence, 2005) 상대습도를 추정 (Modified Penman-Monteith-T 방법)하는 것이 오차가 적어지고 정확도가 높아진다고 하였다. 강원도 지역에서는 Modified Penman-Monteith-T 방법을 이용하였을 때에는 RMSE는 0.49-1.39 mm d-1로 평균 0.75 mm d-1이었고, NSC는 0.37-0.90으로 평균 0.73으로 (Table 4), Penman-Monteith-T 방법과 비교해서 큰 차이를 보이지 않았다. 따라서 강원지역에서 Penman-Monteith-T 방법을 이용할 때에는 Lawrence (2005)가 제안한 것과 같이 이슬점 온도를 조정하기 보다는 원래의 Penman-Monteith-T 방법을 쓰는 것이 나을 것으로 판단된다. Kim et al. (2017)은 안동댐 유역 10지점에서 Penman-Monteith-T 방법을 이용할 때에 이슬점 온도를 일 최저기온으로 대체하여 상대습도를 추정할 수 있다고 하였다.
Table 4. RMSE and NSC for method of Penman-Monteith-T and modified Penman-Monteith-T compared with FAO Penman-Monteith reference evapotranspiration.
강원도 미래 기본증발산량 예측
기후변화 시나리오의 기온 자료와 이 연구의 조정된 Hargreaves 계수를 이용하여 강원지역의 2040년, 2070년, 2100년의 기본증발산량을 추정한 결과, 2007년부터 2017년까지의 기본증발산량의 평균값과 비교하여 2040년에는 2-7%, 2070년에는 7-8%, 2100년에는 8-19% 증가하는 것으로 나타났다 (Table 5). 특히 강릉, 속초, 동해 등 해안 영동지역은 2040년에는 9-16%, 2070년에는 15-17%, 2100년에는 18-31% 증가하여 내륙 영서지역에 비해 증가 폭이 높았다.
결론적으로 Hargreaves 계수를 조정하여 기본증발산량을 추정한 결과, 내륙 영서지방은 12-22% 과대 추정하던 것을 2-5% 과소 추정하였으며, 해안 영동지방은 과소 추정 정도를 12-21%에서 6-7%로 줄일 수 있었다. RMSE는 0.84 mm d-1에서 0.69 mm d-1로 낮아졌고, NSC는 0.69에서 0.78로 높아져서, 오차는 줄고 정확도는 높아졌다. Penman-Monteith-T 방법이나 Modified Penman-Monteith-T 방법과 비교해서는 지역의 기후 특성을 반영하여 Hargreaves 계수를 조정하는 것이 계산이 단순하고 오차가 적으며 정확도는 높았다.
Table 5. Estimated reference evapotranspiration in 2040, 2070, and 2100 based on RCP 4.5 and RCP 8.5 scenario compared with present (average of 2007-2017).
Conclusion
기온, 상대습도, 풍속, 일사량을 모두 측정한 강원도내 11지점을 대상으로, 최근 11년의 기상자료와 FAO Penman-Monteith 공식으로 기본증발산량을 산정하였다. 이 값을 기준으로 하여 Hargreaves 공식의 계수를 보정하였는데, 보정된 Hargreaves 계수는 춘천 등 영서지방은 0.00181-0.00199로 기본값인 0.0023보다 낮았다. 반면에, 강릉 등 영동지방은 0.00275-0.00302로 기본값에 비해서 높았다. Hargreaves 계수를 지역별 기후 특성을 반영하여 보정함으로써 오차의 크기를 나타내는 RMSE는 0.84에서 0.69로 낮아졌고, 추정 정확도를 나타내는 NSC는 0.69에서 0.78로 높아졌다. 이와 같이 강원도의 지역적 기후 특성을 반영함으로써 기본증발산량의 추정이 정밀해지고 신뢰도가 높아질 것으로 판단된다. 따라서 본 논문의 결과는 강원지역에서 농업용수 운용 및 관개, 수자원 관리 등에 유용할 것으로 기대한다.




