Introduction
Materials and Methods
대상토양 특성
관개방법
토양온도 측정
토양온도 추정 모형
Results and Discussion
평균 토양온도
토양온도 진폭
토양온도 예측모형
수정 모형
Conclusions
Introduction
토양 온도는 식물의 생육, 미생물의 활동, 토양 생성과 발달, 물리・화학・생물학적 현상에 폭넓게 영향을 끼치는 요소이며, 종자의 발아와 뿌리의 생장에 직접적으로 영향을 끼치고, 토양미생물의 활성이나 토양수분의 이동, 증발산을 통해 대기의 온도나 습도에도 영향을 끼칠 수 있다 (Kim et al., 2009). 따라서, 토양 내부에서 이루어지고 있는 토양 온도의 변화 특성을 살펴보는 것은 토양에서 발생하는 다양한 현상을 이해하는데 도움이 된다. 토양온도는 하루 또는 년중 변화하는 기온의 영향으로 주기적인 정현함수 (sinusoidal function)로 전파되는 전형적인 특성을 나타내며 (Hillel, 1998), 토양온도의 연간 변화는 Fourier함수를 통해 표현할 수 있고, 1년주기 및 일일 날짜 (Julian date)의 함수로 표현하기도 한다 (Jung et al., 1990). 계절에 따른 변화는 여름에는 최고값, 겨울에는 최저값을 보이는 년 주기의 파동형태로 토양 내로 전달되며 (Ha et al., 1996), 태양복사에너지의 토양 내 열전도 특성으로 인해 토양온도는 지중열류 (soil heat flux)와 일일 최고·최저 값에서 시간지연이 발생한다. Sine이나 cosine 함수처럼 주기적으로 변하는 토양 내부의 에너지 흐름에서 시간지연이 발생한다는 것은 조화함수로 나타낼 수 있는 전형적인 현상으로 태양에너지와 지표면 복사의 영향이 크다 (Hur et al., 2004). 토양깊이별 토양온도를 예측하기 위한 모형은 대부분 일별·년중 모형으로 (Jung et al., 1990; Zheng et al., 1993; Zeynoddin et al., 2019; Mehdizadeh et al., 2020; Shamshirband et al., 2020; Tsai et al., 2020; Wang et al., 2020; Paul et al., 2004) 외기 온도나 태양 복사에너지를 중심으로 토양온도를 예측한다(Zheng et al., 1993; Hur et al., 2004; Paul et al., 2004; Sharma et al., 2010; Dolschak et al., 2015; Barman et al., 2017; Halama et al., 2018). Dolschak (2015)은 토양온도를 예측하기 위한 모형을 크게 프로세스 (process) 기반 모형과 경험 (empirical) 모형으로 구분하였으며, 최근에는 신경그물얼개 (neural network)를 이용하여 토양온도를 예측하고 있음을 설명하고 있으며 (Bilgili et al., 2013; Kisi et al., 2015), 신경그물 얼개에 의한 연구는 토양온도의 주기성과 센서의 발달로 인한 자료의 축적으로 지속적으로 연구가 되고 있다 (Li et al., 2020; Nanda et al., 2020; Shamshirband et al., 2020). 그러나, 이러한 연구들의 대부분은 식물이 자라거나 그렇지 않은 노지토양에서 토양온도를 분석·예측하는 연구들로서, 가온이나 냉방을 해야하는 시설하우스 내 토양의 토양온도에 관해서는 설명하기 어려운 면이 있다. 실외 토양과 시설하우스 토양의 경계 조건은 다르며 (Wang et al., 2020), 피복재의 흡광도와 투과율을 고려하는 것이 필요하다 (Zhang et al., 2020). 이렇듯 시설하우스 내의 토양온도를 예측하는 것은 노지 토양온도를 예측하는 요인들 외에 더 고려할 사항이 있음으로 인해 연구결과가 많지는 않은 상황이다.
본 연구는 작물이 재배되고 있는 관개를 실시하는 시설하우스 내의 토양에서 동계에서 봄까지의 재배기간 시간의 변화에 따른 토양 깊이별 토양온도의 특성을 분석하고 이를 예측하기 위한 모형을 작성하고자 수행되었다.
Materials and Methods
대상토양 특성
토양온도 측정을 위한 시험대상지는 경북 상주에 위치한 연동형 시설하우스로서 강서통 (Gangseo Series; coarse loamy, mixed, non-acid mesic family of Fluvaguentic Eutrudepts)으로 분류되고 논으로 이용되는 토양이었으나 시설재배지로 전환되어 오이를 재배하는 농가토양이다. 이 토양의 물리・화학적 특징은 다음의 Table 1과 같다. 토양분석은 농촌진흥청 국립농업과학원의 토양분석방법을 준용하였다 (RDA, 2000). pH는 일반적인 우리나라 토양의 적정범위인 6.0 - 6.5보다는 낮은 값을 보였고, Ca 함량은 적정범위인 5.0 - 6.0 cmolc kg-1 보다 높다. 표토의 용적밀도는 유기물 투입으로 인해 0.99 g cm-3를 보였고, 그로 인해 고상은 낮은 값을 보였으며, 심토의 용적밀도는 상대적으로 표토보다 높게 나타났고, 그로 인해 고상도 높은 값을 나타내는 토양이다.
Table 1.
Soil chemical and physical properties of experimental site.
관개방법
작물 재배를 위한 관개방법은 물 소비량이 많은 오이 재배의 특성을 감안해 15 kPa과 20 kPa을 관개시점으로 설정하였으며, 관개 깊이는 토심 15 cm, 관개종료 시간은 관개시작 후 10분으로 하였다. 토양수분 장력을 측정할 수 있는 압력 센서가 부착된 텐시오미터를 활용하여 관개를 조절하였다.
토양온도 측정
토양 온도 측정은 토양 수분과 토양온도를 동시에 측정할 수 있는 센서 (Sentek Drill & Drop Probe)를 활용하였으며, 10 cm 단위로 토양 깊이 60 cm까지 측정할 수 있는 센서 6개가 프로파일 형태로 구성되어 있다. 토양온도 측정기간은 오이 수확 기간인 2019년 12월 13일부터 2020년 5월 28일까지이며, 측정시간은 10분 단위로 측정 후 시간단위로 평균하여 분석하였다.
토양온도 추정 모형
토양 온도를 예측하는 모델은 다음의 Eq. (1)과 같은 Fourier 급수 (Jung et al., 1990)를 기본 방정식으로 사용하였으며, 수치해석 방법 (numerical method)을 통해 계수를 산정하였다. Fourier 급수는 주기함수를 삼각함수의 급수로 나타낸 것으로서 파장이 주기적으로 나타나는 함수에 사용된다.
여기서, 는 지온을 의미하여 는 초기 값을 나타내고, 과 은 진폭, 는 주기, 는 위상을 나타낸다.
Results and Discussion
평균 토양온도
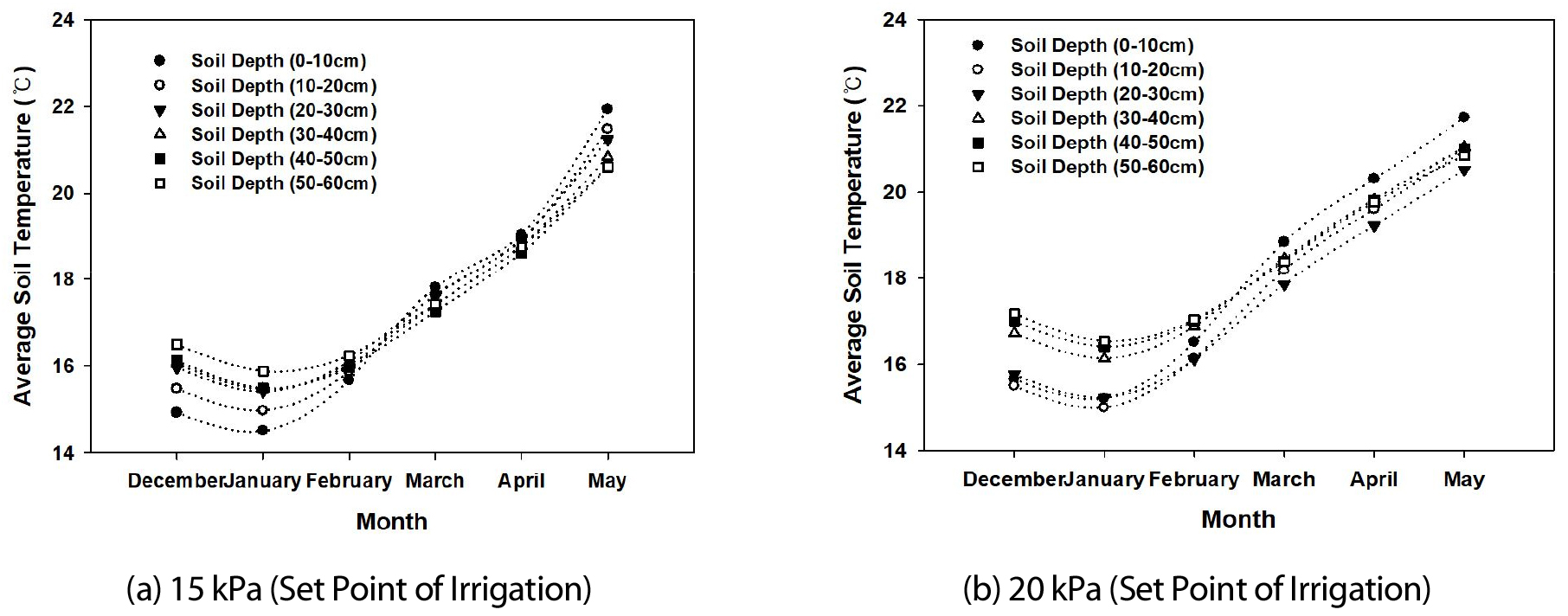
시설하우스 내의 평균 토양 온도의 변화는 처리별・시기별로 다르게 나타났다 (Fig. 1).
15 kPa 및 20 kPa 관개 처리구에서 평균 토양 온도는 1월에 가장 낮았다가 2월부터 5월까지 지속적으로 상승하는 경향을 보여주고 있으며, 지표면으로부터 10 cm 깊이에서 가장 낮은 값을 보이다가 3월부터 가장 높은 값을 보여주고 있다. 지표면으로부터 50 - 60 cm 깊이에서의 토양 온도는 15 kPa에서는 12월, 1월, 2월까지는 가장 높은 값을 보이다가 3월, 4월을 지나면서 다른 깊이의 토양 온도에 비해 낮아지다가 5월에는 가장 낮은 값을 보여주고 있으며, 20 kPa에서는 상대적으로 20 - 30 cm 깊이에서 낮은 값을 나타내고 있다. 동일 시기의 깊이별 최고와 최저의 토양 온도 편차는 약 1.5°C로 큰 차이를 나타내고 있지는 않다.
토양온도 진폭
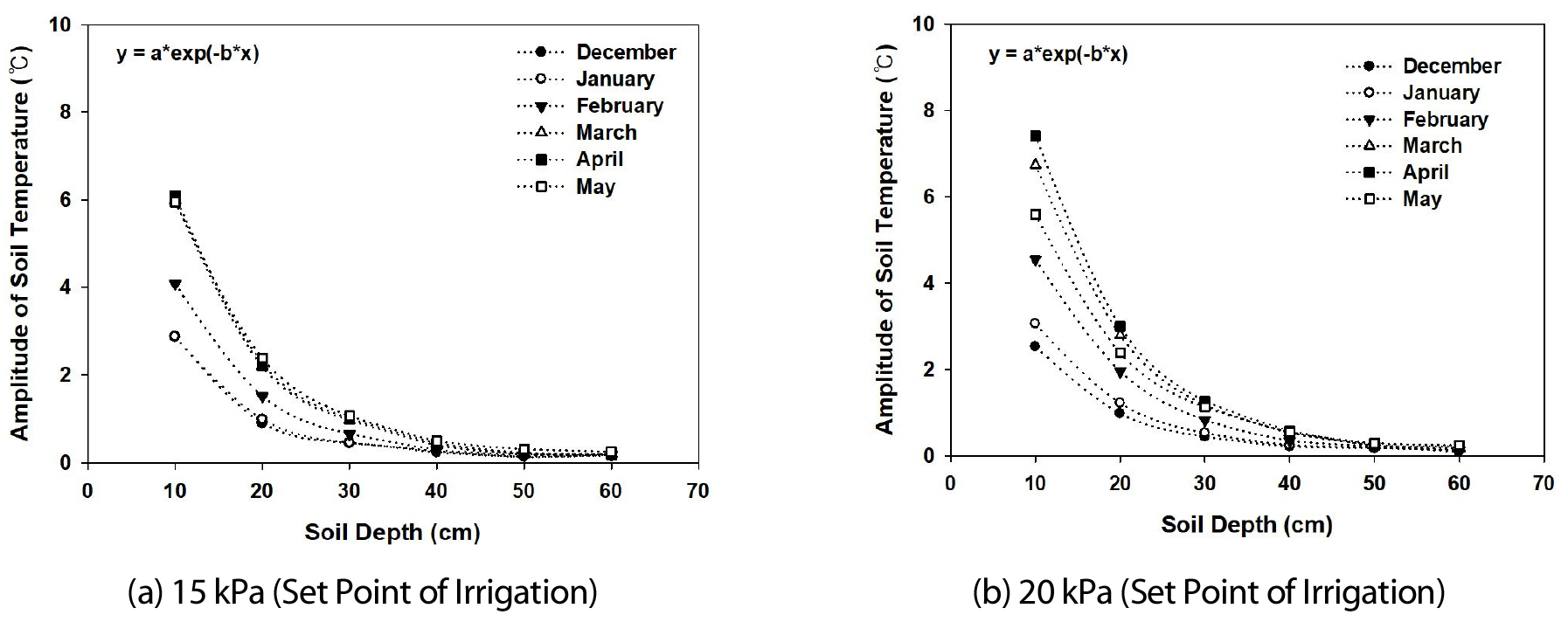
월별 최고 값과 최저 값의 차이를 나타내는 진폭 (Amplitude)의 변화는 Exponential 감소 함수의 형태를 나타내고 있다 (Fig. 2).
진폭의 변화는 지표면으로부터 10 cm 깊이에서 가장 크게 나타나고 있었으며, 토양의 깊이가 깊어질수록 진폭의 변화는 점점 줄어들어 0에 가까와 지는 것으로 나타났다. 특히, 40 - 50 cm와 50 - 60 cm 깊이에서는 토양 온도의 변화가 거의 없음을 알 수 있다. 진폭의 변화가 가장 큰 시기는 4월이었으며, 진폭의 변화가 가장 작은 시기는 12월이었다.
Fig. 2에 나타난 월별 토양 깊이에 따른 토양 온도 진폭의 변화는 다음의 Eq. (2)와 같은 함수로 나타낼 수 있다.
여기서, 는 토양 온도의 진폭 (amplitude)이고 는 토양 깊이 (cm), a와 b는 상수이다.
관개 처리에 따른 토양깊이별 토양온도 진폭의 변화를 월별로 감쇄의 정도를 분석하였을 때 15 kPa과 20 kPa 모두에서 결정계수 (coefficient of determination)가 0.9894에서 0.9996까지 아주 높은 통계적 유의성을 보여주고 있으며, a는 12월 1월이 작고, b는 15 kPa에서는 12월 1월이 조금 크고, 20 kPa에서는 5월이 가장 작은 값을 보여주고 있다 (Table 2).
Table 2.
Statistical characteristics on amplitude of soil temperature by soil depths.
토양온도 예측모형
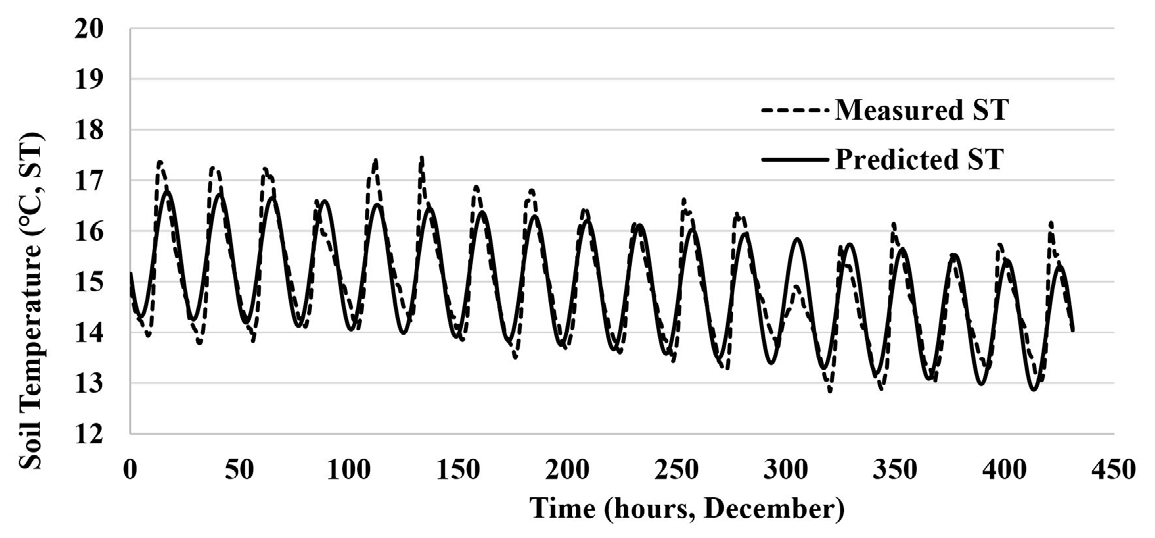
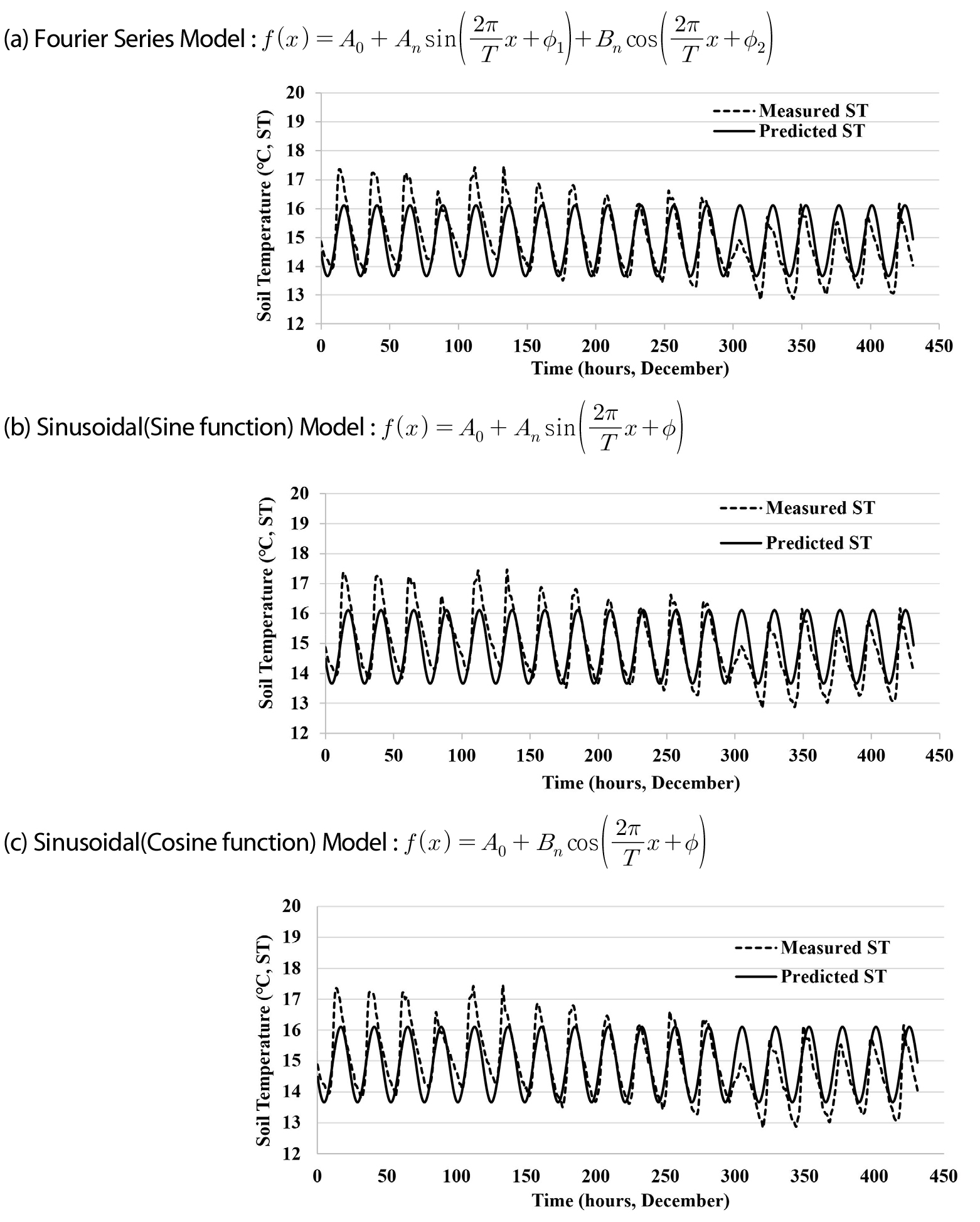
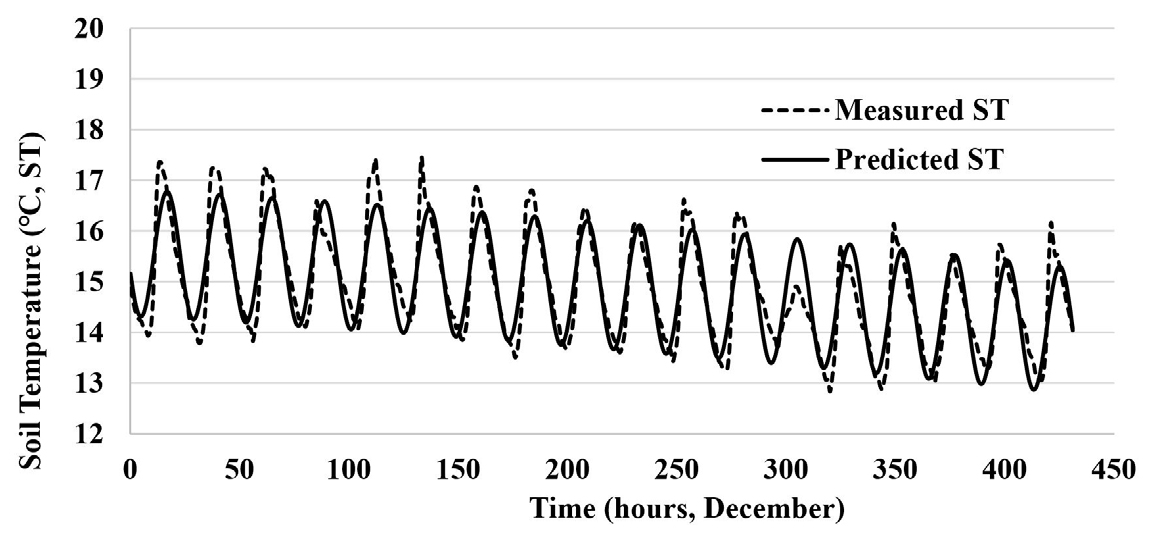
토양 온도를 예측하는 모형은 기본적으로 Fourier 급수를 활용하였는데, Fourier 급수가 Sine과 Cosine 함수의 조합으로 이루어져 있어 토양 온도를 예측하고 표현함에 있어 이 두개의 함수가 모두 활용이 되는지를 점검하고 정현파 (sinusoidal) 모형 (Hillel, 1998)과는 다른 것이 있는지 평가를 해보고, 결과가 유사하다면 Fourier 급수보다는 상대적으로 간단한 정현파 모형으로 예측 모형을 작성하는 것이 효율적일 것이다. 정현파는 Sine 함수로 된 주기신호를 말한다. 수치해석적 방법으로 분석한 Fourier 급수와 정현파 모형의 결과는 Fig. 3에 나타나 있다. 이것은 15 kPa 관개 처리구의 12월 기간 동안의 0 - 10 cm 토양 깊이의 시간단위 자료에 대한 분석결과이다.
모든 모형이 반복되는 주기를 나타내며, 일정한 진폭을 갖고 있고, 측정 초반에는 약간 과소 예측 경향이 있으며, 측정 후반의 경우에는 낮아지는 온도에 대한 경향이 제대로 반영되지 못하고 있다. 통계분석을 통하여 측정 값과 예측 값을 비교해 보면 (Table 3) 더욱 뚜렷하게 특성을 알 수 있다. 세개의 모형 모두 초기 값을 나타내는 의 값이 동일하고, 주기를 나타내는 값 (24.0252시간)도 동일해 결과적으로 (a), (b), (c) 모두 동일한 그림으로 나타난다. 결정 계수()도 0.6443으로 동일하며, 측정값과 예측 값의 오차의 제곱의 합을 의미하는 SSE도 동일하다. 또한, 정현파 모형인 (b)와 (c)는 위상() 만 차이가 있지 초기값, 진폭과 주기 모두 동일한 값을 보여주고 있다. 이러한 위상 차이는 실제 Sine과 Cosine 함수가 동일해질 수 있는 위상 차이를 의미한다. 결론적으로, Fourier 급수와 정현파 모형을 비교하였을 때 복잡하고 계수가 많은 Fourier 급수 모형보다는 Sine과 Cosine 중 하나의 정현파 모형을 사용하는 것이 유용해 보인다.
Table 3.
Statistical characteristics on measured & predicted soil temperature by time.
수정 모형
정현파 모형의 유용함에도 불구하고 동일한 진폭과 기울기가 없는 특징으로 Fig. 3에는 시간이 흐름에 따라 하락하는 토양 온도 경향을 제대로 반영하고 있지 못하다. 12월 후반으로 갈수록 토양 온도가 낮아지는 현상을 예측할 수 있어야 개선된 모형으로서 의미가 있으므로 이에 대한 해결 방안이 필요하다. Fig. 4는 온도가 낮아지는 경향을 예측할 수 있도록 정현파 모형을 수정한 모형과 실측 값을 비교한 것이다. 수정한 모형은 다음의 Eq. (3)과 같이 나타낸다.
여기서, C는 1차함수의 계수이고, D는 2차함수의 계수이다.
Eq. (3)은 정현파 함수인 Sine함수에 토양 온도가 하락하는 경향을 나타낼 수 있도록 음의 2차 방정식을 조합한 것이다. 예측 값과 실측 값을 비교해보면 앞에서 분석했던 Fourier 급수 모형이나 정현파 모형보다 더욱 개선되어 있음을 알 수 있다. 초기값이 높아지고 진폭도 더 커졌으며, 12월 후반으로 갈수록 감소하는 토양 온도의 변화를 잘 모사하고 있음을 알 수 있다.
Fig. 4에서 나타나는 경향을 통계적으로 분석해 보면 다음의 Table 4와 같다. 초기 값은 15.5694로 앞선 (a), (b), (c) 모형보다 0.6824 높고, 진폭도 (b), (c) 모형보다 0.0271 더 커졌으며, 주기는 비슷하고 위상은 (b) 모형과 약간의 차이가 있음을 알 수 있다. 토양 온도가 하강하는 특성을 나타내는 2차함수의 계수는 작은 값을 보여주고 있으나 경향을 아주 잘 모사하고 있으며, 결정 계수가 0.8178, SSE가 91.3075로 수정 모형이 통계적으로 훨씬 더 개선되었음을 확인 할 수 있다.
Table 4.
Statistical characteristics on measured & predicted soil temperature by time.
| A0 | An | T | ϕ | C | D | R2 | SSE |
| 15.5694 | 1.2492 | 24.0250 | 3.4780 | 0.0023 | 2.92・ | 0.8178*** | 91.3075 |
Fig. 1에는 1월을 지나 2월부터 토양 온도가 상승하고 있는 것을 보여주고 있다. 이것은 시간단위로 분석하는 토양 온도에서도 동일한 경향을 보여주고 있는데, Fig. 5에서는 3월의 상승하고 있는 시간단위 토양 온도 변화를 보여주고 있다. 또한, 그러한 토양 온도를 예측하기 위해 Eq. (3)과 유사한 양의 2차함수를 정현함수와 조합을 하여 토양 온도가 상승하는 경향을 예측하고자 하였다. 3월의 토양 온도를 예측하기 위하여 수정한 모형은 Eq. (3)과 유사하지만 2차함수가 상승하는 경향을 반영하도록 양의 2차 함수로 표현하고 있다 (Eq. 4).
여기서, C와 D는 Eq. (3)에서와 마찬가지로 1차함수와 2차함수의 계수이다.
Fig. 5에 나타나 있는 것처럼 정현함수와 2차함수의 조합은 토양 온도 변화를 잘 모사하고 있음을 보여주고 있으며, 3월의 온도가 초반에 비해 후반부로 갈수록 상승하고 있는 경향도 잘 모사하고 있음을 확인 할 수 있다. 이러한 결과를 확인하기 위해 측정 값과 예측 값에 대한 분석을 실시하였다.
그 결과는 다음의 Table 5와 같다. 초기 값은 16.3692로 앞선 Eq. (3) 모형보다 0.7998 높고, 진폭도 약 2.2배 가량 커졌다. 주기와 위상은 비슷하고, 토양 온도가 상승하는 특성을 나타내는 2차함수의 계수는 Eq. (3)처럼 작은 값을 보여주나 경향을 아주 잘 모사하고 있으며, 결정 계수가 0.8192로 통계적으로 아주 유의하게 수정 모형의 유용성을 확인 할 수 있다.
Table 5.
Statistical characteristics on measured & predicted soil temperature by time.
| A0 | An | T | ϕ | C | D | R2 | SSE |
| 16.3692 | 2.7674 | 24.0005 | 3.4776 | 0.0035 | 7.29・ | 0.8192*** | 767.456 |
이러한 결과를 종합하면 토양 온도를 예측하는 수정 모형은 정현파와 2차함수를 조합하는 모형이 될 수 있으며, 온도가 하강할 때는 2차함수에 음의 계수를, 온도가 상승할 때는 양의 계수를 적용하고, 온도 변화의 기울기가 없는 경우에는 2차함수의 계수를 0으로 적용하면 정현파와 동일 한 모형으로 작용할 수 있으므로, 결과적으로 토양온도를 예측하는 수정 모형은 다음의 Eq. (5)와 같이 표현된다.
이러한 토양 온도 예측 모형을 바탕으로 12월부터 수확이 완료되는 5월까지의 토양 온도를 실측한 값과 수치해석을 통해 예측한 값을 분석한 결과는 다음의 Table 6 (15 kPa), Table 7 (20 kPa)과 같다. 앞서 설명한 것처럼 기울기가 없는 경우에는 1월 20 - 30 cm 경우처럼 2차함수 계수가 0으로 수렴하고, 40 - 50 cm, 50 - 60 cm의 경우에는 다른 깊이에서는 주기가 24시간 근처의 값을 나타내는데 반해 토양 온도의 변화가 미미한 관계로 변화 주기는 훨씬 큰 값을 보여주고 있다.
Table 6.
Statistical characteristics on measured & predicted soil temperature by time at 15 kPa irrigation treatment.
Table 7.
Statistical characteristics on measured & predicted soil temperature by time at 20 kPa irrigation treatment.
Conclusions
시설재배 토양에서의 토양온도는 겨울에는 일정온도를 유지하기 위해 가온을 하거나 여름철에는 냉방을 하므로 외기에서의 토양온도 변화와는 다르게 반응한다. 본 연구는 시설재배 토양에서 토양 깊이별 토양 온도 변화를 살펴보고 이를 예측하기 위한 모형을 작성하기 위해 수행하였다. 15 kPa, 20 kPa로 관개 처리가 된 오이를 재배하는 시설재배 사양토에서 0 - 10, 10 - 20, 20 - 30, 30 - 40, 40 - 50, 50 - 60 cm 깊이에서의 토양 온도를 시설오이 수확기인 2019년 12월 13일부터 2020년 5월 28일까지 측정하고 분석한 결과, 평균 토양 온도는 1월에 가장 낮았다가 2월부터 5월까지 지속적으로 상승하며, 0 - 10 cm 깊이에서 변동이 가장 크고 3월 이후부터 가장 높은 값을 보여주고 있다. 최고・최저 온도의 편차인 진폭은 0 - 10 cm에서 50 - 60 cm 깊이로 깊어질수록 감소하는 경향이었으며, 40 - 50 cm 이후는 온도 변화가 거의 없는 것으로 나타나고 있다. 이러한 감소 경향은 토양 깊이에 대한 Exponential 감소 함수로 나타낼 수 있었다. 토양의 깊이가 깊어질수록 온도변화가 거의 없는 것은 토양 외부로부터의 복사에너지가 침투할 수 있는 한계 깊이가 있음을 의미하며, 토양온도에 대한 평균평방오차가 토양의 깊이가 깊어질수록 더 작아진다는 Jung et al. (1990)의 연구결과와 동일한 경향을 보여준다. 토양 온도를 예측하는 모형은 기본적으로 Fourier 급수를 활용할 수 있으나, 정현파 (Sinusoidal) 함수 모형과 비교한 결과 통계적으로 동일한 값을 보여 계수의 개수가 적은 정현파 함수가 더 유용함을 알 수 있었다. 그러나, 정현파 함수는 기울기가 있는 온도변화를 예측하는 것에는 정확성이 떨어져 온도변화 기울기가 반영될 수 있는 수정 모형이 필요하였으며, 분석결과 다음과 같은 모형으로 수정할 수 있었다.
이 모형은 주기성을 나타내는 정현파 함수에 온도변화의 기울기를 감안할 수 있는 2차함수가 조합된 모형으로서 2차함수 계수가 양일 경우에는 상승하는 경향을, 계수가 음일 경우에는 감소하는 경향을 모사할 수 있어 온도의 상승이나 하강 시기에 적용할 수 있고, 2차함수의 계수를 0으로 하면 온도변화가 없는 시기도 예측할 수 있는 특징이 있다. 이 모형은 대부분의 토양온도 모형이 설명하기 어려운 온도 상승과 하강하는 시기의 변화를 나타낼 수 있는 특성이 있다. 다만, 온도변화 폭이 큰 4월과 5월에는 예측 정확도가 조금 떨어지는 경향이었으나, 측정기간 동안 토양 깊이별 토양 온도를 대체적으로 잘 모사하고 있었다. 본 연구는 토양 온도를 예측함에 있어 열전도의 주요 인자인 토양수분을 고려하지는 못한 한계점이 있기는 하나, 토양 온도변화 기울기를 반영할 수 있다는 것과 시설재배 토양에서의 온도변화를 분석・예측 하였다는데 의의가 있으며, 온도변화 기울기를 감안할 수 있다는 장점은 외기 조건에서의 토양온도 예측에도 활용 될 수 있을 것이다.