Introduction

기후변화에 수반되는 이상 기상 등에 의해 토지가 집약적으로 이용되고 있는 우리나라에서 다양한 오염원에 기인한 수질 오염 문제가 더욱 심각해지고 있다 (Jeon, 2015; Kang and Lee, 2019). 특히, 농경지, 축산, 산림, 주거가 복합적으로 구성되어 있는 농촌지역은 오염원이 다양하고 오염물질의 유출 경로가 복잡하여 수질 오염 관리가 더욱 어렵다 (Sun et al., 2012; Jeon, 2015; Nam et al., 2019). 따라서, 농촌지역과 같은 복합토지이용 유역의 수질 관리를 위해서는 수질 오염원을 평가할 수 있는 기술 개발이 요구되는데, 특히 각 오염원 별 특성을 반영하는 추적자 (Tracer)를 활용하여 수질 오염원의 기여도를 평가하는 기술이 주목받고 있다 (Murphy and Morrison, 2014).

다양한 추적자 중 안정성동위원소를 활용하는 연구가 여러 국가에서 진행되어왔는데, 우리나라에서도 질소 (N) 동위원소비 (¹⁵N/¹⁴N, δ¹⁵N)를 이용하여 다양한 토지이용형태별로 지표수와 지하수의 오염원을 추정한 바 있다 (Yoo et al., 1999; Hong et al., 2001; Lee et al., 2003; Choi et al., 2007, 2011). 하지만, δ¹⁵N만을 오염 추적자로 활용할 경우에 오염원 별δ¹⁵N 값이 중첩하는 문제와 세 가지 이상의 오염원 구명은 불가능한 문제가 있어, 농촌지역과 같은 복합토지이용 유역의 오염원을 구명하는데 적용하기 어렵다 (Choi et al., 2017). 이러한 한계점을 극복하여 농촌지역과 같은 복합토지이용 유역의 수질 오염원 규명을 위해서는 δ¹⁵N과 탄소 동위원소비 (¹³C/¹²C, δ¹³C), 그리고 탄소와 질소를 포함한 다종의 원소 함량 등 다양한 수질 화학 지표를 추적자로 사용할 필요가 있다 (Jeon, 2015). 수질 오염 원인자로 작용하는 다양한 오염원들은 물질의 구성 및 생성, 순환 과정의 차이에 의해 동위원소 및 원소 함량이 상이할 수 있기 때문에 오염원과 수질 시료의 동위원소 및 원소 함량을 비교 분석함으로써 복합토지이용 유역의 수질 오염원 추적에 활용할 수 있다 (Choi et al., 2017; Park et al., 2020; Park et al., 2021). Jeon (2015)은 농촌지역 유역의 오염원 별 동위원소비 및 원소 함량비를Tree model에 적용하여 하천수의 오염원 별 기여도를 평가한 바 있다. 오염원 분류를 위한 Tree model에서는 여러 오염원을 대상으로 다양한 화학 추적자를 분석하여, 추적자별 분포 범위가 유사한 오염원을 순차적으로 두 가지 집단으로 구분하고, 각 집단의 추적자 평균값을 두 가지 집단을 구분하는 end-member (각 오염원 또는 오염원 집단별 추적자의 대표 값)로 사용하여 순차적으로 오염원 집단의 기여도를 평가하여 최종적으로 다양한 개별 오염원의 기여도를 평가한다 (Spruill et al., 2002). 하지만, Tree model은 두 집단 간의 상대적 오염기여도를 단계별로 평가하기 때문에, 동일 집단내에 포함된 오염원 별 기여도를 직접적으로 평가할 수 없고 통계적 신뢰도 확보가 어렵다는 한계가 있다 (Spruill et al., 2002).

이에 반해, 동위원소 혼합 모델 (Isotope mixing model)을 이용하여 다중 오염원의 기여도를 동시에 평가 가능한 R 기반의 SIAR (Stable Isotope Analysis in R) 모델은 산출된 잠재 요인의 기여도에 대한 통계적 신뢰구간 확보가 가능하여 오염원 평가 결과의 신뢰도가 높은 장점이 있다 (Parnell et al., 2013; Wang et al., 2019). SIAR 모델은 애초 동위원소를 이용하여 먹이 그물의 역학을 구명하기 위하여 개발되었지만, 최근 여러 연구에서 복합토지이용 유역의 지하수나 지표수의 질소오염원을 구명하거나 (Xue et al., 2012; Matiatos, 2016; Yu et al., 2020; Yuan et al., 2020) 유역의 유기물 오염원을 구명하는 연구 (Lu et al., 2016) 등에 활용된 바가 있어 비점오염원 구명 연구에도 적용이 가능한 것으로 확인되었다. SIAR 모델은 동위원소비뿐만 아니라 원소 함량비를 함께 입력 변수로 활용하면 잠재적 오염원의 기여도를 보다 더 정확하게 정량화할 수 있도록 개발되었기 때문에 (Parnell, 2008), 비점오염원의 원소 함량비도 추적자로 활용할 수 있다. 예를 들면, Lu et al. (2016)은 유역의 유기물 오염원을 구명하기 위해 C/N을 이용하였으며, Garzon-Garcia et al. (2017)은 저수지 침전물의 오염원 구명을 위해 탄소 및 질소 함량 (총탄소와 총유기탄소, 총질소 함량)등을 추적자로 이용하였다.

이와 같이 SIAR 모델은 비점오염원의 동위원소비와 원소 함량비를 이용하여 오염원을 추적하고 기여도를 평가하는데 활용될 수 있지만, 현재까지 진행된 연구에서는 SIAR 모형의 결과를 그대로 사용하여 복합토지이용 유역의 오염원을 추적하였고, SIAR모형의 정확도가 이론적으로 검증된 바가 없다. 따라서, 비점오염원 기여도 평가 연구에서 SIAR 모형의 활용도 확대를 위해서는 다양한 시나리오별로 SIAR 모형의 정확도에 대한 이론적 검정이 필요한다. 본 연구는 복합토지이용 유역의 비점오염원 기여도 평가를 위한 SIAR 모형의 정확도를 검증하고 적합한 SIAR 모형 구동 방안을 제시하고자 하였다. 또한, 실제 농촌유역에서 조사한 결과를 활용하여SIAR 모형을 구동함으로써 복합토지이용 유역의 비점오염원 기여도 평가를 위한 SIAR 모델의 적용 가능성을 평가하였다.

Materials and Methods

SIAR 모형

SIAR모형은 2008년 Bayesian 이론을 기반으로 하여 생태환경 연구 분야에서 물질Sink (예, 수질)에 대한 Source (오염원)의 잠재적인 기여도를 평가하기 위해 개발되었다 (Parnell, 2008). 모델을 통해 정량화된 잠재 요인의 기여도는 다음과 같이 표현된다 (Parnell et al., 2010).

여기서, X_ij는 Sink i (=1, 2, 3, ···, I)의 j (=1, 2, 3, ···, J) 동위원소비 또는 원소 함량비이다. Sjk와 Cjk는 각각 Source k (=1, 2, 3, ···, K)의 j 동위원소비 또는 원소 함량비와 동위원소 분할 (fractionation) 지수이며, 이들은 일반적으로 각각 평균 μjk와 표준편차 ωjk2, 평균 λjk와 표준편차 τjk2의 정규분포를 따른다. Pk는 SIAR 모형에서 추정하는 오염원 k의 기여도이다. εij는 오차이며, 이는 평균 0과 표준편차 σj2 정규분포를 따른다. 따라서, SIAR 모델링을 위해 입력되는 변수는 총 3종류인데, 첫째, 조사 유역의 수질 시료 (Sink)에 대한 동위원소비 또는 원소 함량비와 같은 추적자의 평균, 둘째, 오염원 추적자의 end-member의 평균과 표준편차, 셋째, 동위원소분할지수의 평균값과 표준편차로 구성된다. 이 때, 동위원소분할 작용을 고려하지 않을 경우, 분할 지수를 “0”으로 기입하여도 모형은 구동할 수 있다 (Parnell, 2008).

SIAR 모델의 기반인 R 프로그램은 무료 공용프로그램으로 http://www.r-project.org/에서 설치 가능하다. R 프로그램은 스크립트를 통해 명령문을 이용하여 모델을 구동하거나 결과를 도식화 하기 때문에 명령문에 대한 학습이 필요하며, 학습을 위한 자료는 프로그램 설치 홈페이지에서 얻을 수 있다.

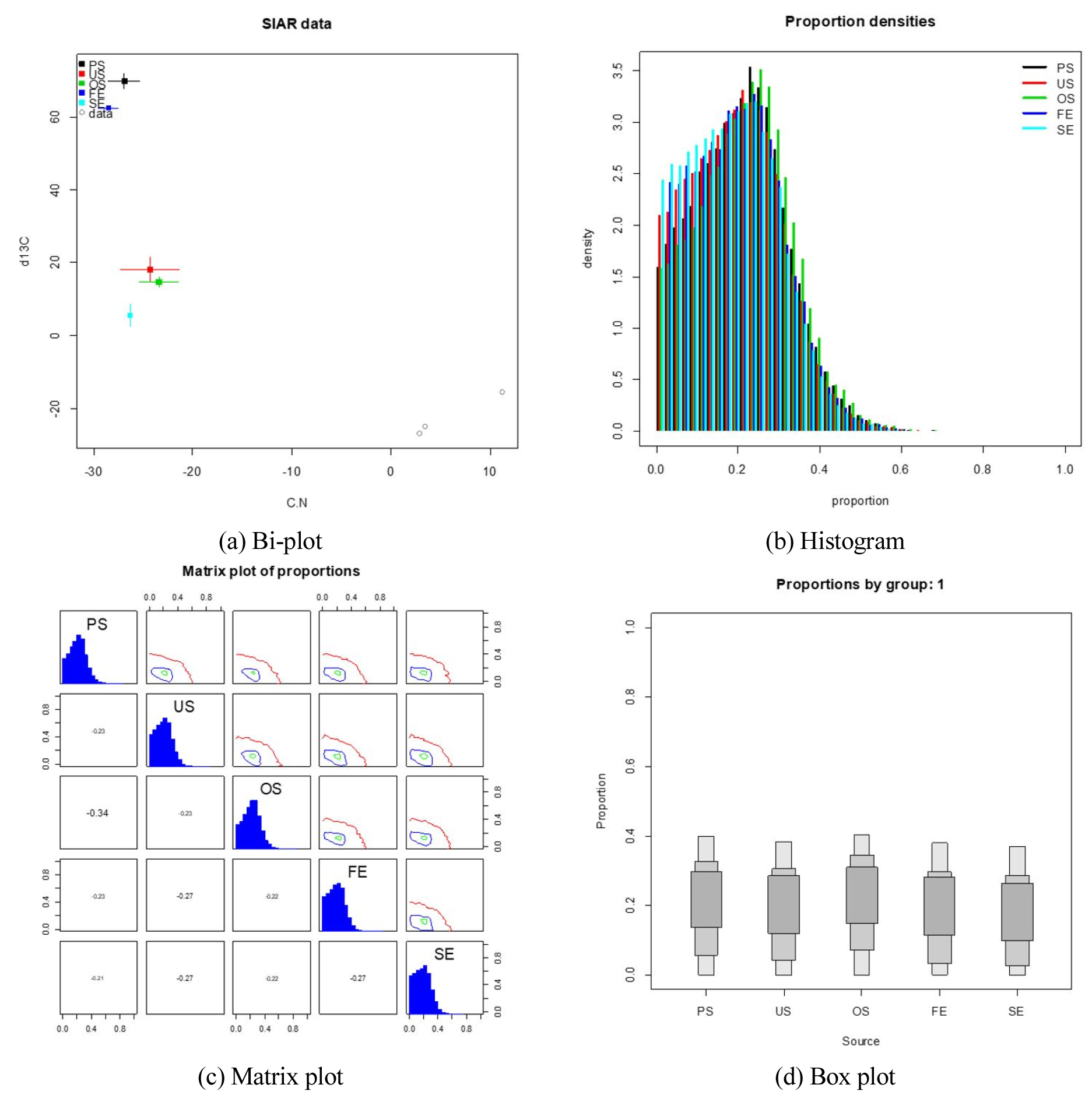
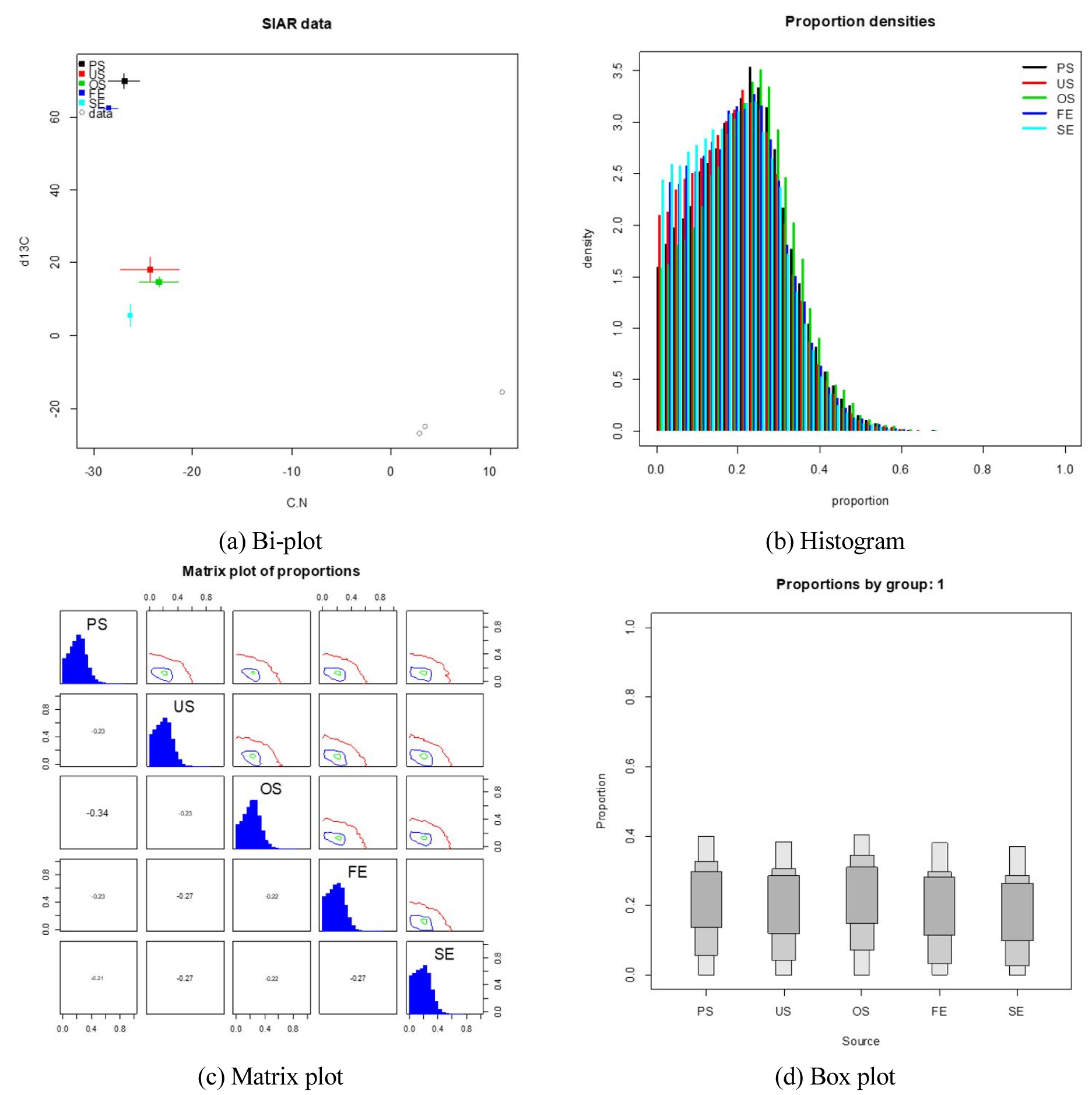
R프로그램에서 SIAR 패키지 설치 및 데이터 입력, 모델 구동 등에 필요한 명령어는 Table 1에 정리하였다. SIAR 패키지 외에도 엑셀 패키지를 설치하여 엑셀에 입력된 데이터를 SIAR 패키지의 입력 값으로 전환할 수도 있지만 (Nam et al., 2019), 본 연구에서는 엑셀 파일을 텍스트 형식의 파일로 변환하여 SIAR 패키지에 입력하였다. R프로그램을 이용하여 SIAR 모형의 분석결과를 행렬도 (bi-plot), 히스토그램, 산점도 (matrix plot), 상자그림 (box plot)으로 도식화할 수 있으며 (Fig. 1), 수치화하여 텍스트 형식의 파일로 저장할 수도 있다. 저장한 텍스트 형식의 파일은 파일 형식을 변환하여 엑셀로 데이터를 추출 및 가공할 수 있다.

Fig. 1

Examples of diagrams of model output of SIAR: (a) bi-plot, (b) histogram, (c) matrix plot, and (d) box plot.

가상 데이터를 이용한 SIAR 모형의 정확도 검증

모형의 정확도 평가를 위해서 논, 밭, 과수원, 생활하수, 산림 등 5개의 가상의 오염원을 설정하고 δ¹³C, δ¹⁵N, C/N, N/P, Na/Ca를 추적자로 사용하였다 (Table 2a). 오염원과 추적자의 종류는 SIAR 모형의 실제 유역 적용에 활용된 Jeon (2015)의 자료에 근거하여 선정하였다. Jeon (2015)에 의하면 논-밭-과수원-산림은 탄소와 질소의 공급원과 각각의 투입량과 손실량 차이에 의해 δ¹³C, δ¹⁵N, C/N, 그리고 N/P가 상이 하였으며, 생활하수는 특이적으로 Na/Ca이 높았다. SIAR 모형은 두 가지 시나리오로 검증하였는데, 시나리오 1에서는 모형에 활용되는 추적자 end-member의 종류와 개수에 따른 정확도를 검증하였으며, 시나리오 2에서는 시나리오 1의 결과를 확장하여 오염원 개수가 상이한 조건에서 각 오염원 별 기여도가 달라졌을 때의 정확도를 검증하였다.

시나리오 1에서는 오염원을 5개로 고정하고 각 오염원의 기여도가 상이한 3개의 유역 (Sink 1–3) (Table 2b)을 대상으로 추적자 end-member의 종류와 수를2‒5개로 달리하여 모두 8개의 end-member 경우의 수 조합으로 구성하였는데, 조합에는2가지 동위원소비 (δ¹³C와 δ¹⁵N)를 기본으로 하고 나머지 C/N, N/P, Na/Ca를 계승적 (factorial)으로 포함시켰다. 사용한 end-member 조합은 end-member 2개 (δ¹³C-δ¹⁵N), 3개 (δ¹³C-δ¹⁵N-C/N, δ¹³C-δ¹⁵N-N/P, δ¹³C-δ¹⁵N-Na/Ca), 4개 (δ¹³C-δ¹⁵N-C/N-N/P, δ¹³C-δ¹⁵N-C/N-Na/Ca, δ¹³C-δ¹⁵N-N/P-Na/Ca), 5개 (δ¹³C-δ¹⁵N-C/N-N/P-Na/Ca)였다. 시나리오 2에서는 추적자 end-member를 5개로 고정하고, 오염원의 종류가 각각 3, 4, 5개인 3개 유역에서 각 오염원의 오염 기여도가 5가지로 변하는 15개의 세부시나리오 조건 (Table 2c)으로 모형의 정확도를 검증하였다. 일반적으로 SIAR에서 요구하는 추적자 end-member개수는 (n‒1) 개이지만 (Parnell, 2008), 시나리오 2에서는 추적자 end-member의 종류와 개수의 영향이 배제된 조건에서 개별 오염원의 기여도가 달라질 때 SIAR 모형의 정확도를 검증하였다.

오염원 (Source)과 각 수질 시료 (Sink)의 end-member를 SIAR 모형에 입력하여 각 오염원의 기여도를 산출하였으며, end-member에 대한 분할 지수는 0으로 하여 분할 작용은 고려하지 않았다. SIAR 모형의 정확도 검증을 위해 가상 시나리오에서 설정한 각 오염원의 기여도 값 (설정치)과 SIAR 모델을 통해 산출된 오염원의 기여도 값 (예측치)을 회귀 분석을 통해 비교하였으며, 결정 계수 (r²)가 0.90이상일 때 모형의 신뢰도가 높다고 판단하였다.

실제 유역 분석 자료를 이용한 SIAR 모델의 적용성 검토

이상과 같은 시나리오에서는 각 오염원 별로 수질 시료의 특정 오염물질 (예를 들면, 총탄소, 총질소, 총인)에 대한 기여도 보다는 잠재적 전체 오염원의 오염 기여도를 평가할 수 있다. 하지만, 농촌지역 수질 관리를 위해서는 잠재적 오염원 기여도 보다는 특정 오염원에 대한 각 오염원 기여도 평가가 필요하다. 이를 위해, 영농-축산-주거-산림이 복합적으로 구성된 전남 장성군 풍영정천 유역에서 수행된 Jeon (2015)의 연구 결과를 활용하여 복합토지이용 유역 수질의 총탄소, 총질소, 총인에 대한 오염원 별 기여도 평가에서 SIAR 모델의 적용성을 검토하였다. 이 유역에는 5가지의 오염원 (논, 밭, 과수원, 생활하수, 산림)이 있는 것으로 조사되었다. Jeon (2015)의 결과 중 SIAR 모형 분석을 위해 필요한 유역의 수질 시료 및 오염원의 end-member 데이터는 Jeon (2015)의 결과를 활용하였다 (Table 3). Jeon (2015)은 이 유역으로 유입되는 오염물질의 탄소와 질소, 인 (P) 함량 및 탄소와 질소 동위원소비를 조사하였으며, 약 5개월간 유역의 수질 시료를 정기적으로 채취하여 동일한 항목을 조사하였다.

본 연구에서는 Jeon (2015)의 연구결과 중 대표적인 수질오염물질 측정 항목인 탄소, 질소, 인 함량이 상대적으로 높은 하천 수질 시료에 대해 SIAR 모델을 적용하여 총탄소, 총질소, 총인에 대한 5개 오염원의 기여도를 평가하였다 (Table 3). 총탄소, 총질소, 총인 오염원 기여도 평가를 위해 원소 함량비 (C/N, N/P, C/P)와 동위원소비 (δ¹³C, δ¹⁵N)를 추적자로 추출하여 각각의end-member를 사용하였으며, end-member에 대한 분할 지수는 0으로 가정하였다. 총탄소, 총질소, 총인 오염 기여도 평가에는 각 오염물질과 관련도가 높은 C/N-C/P-δ¹³C (총탄소), C/N-N/P-δ¹⁵N (총질소)와 N/P-C/P (총인)를 추적자로 선정하여 각 추적자의 평균값을 end-member로 사용하였다. Sink 1, 2, 3 수질 시료의 총탄소 농도는 각각11.9±2.5, 6.7±1.3, 5.3±1.6 mg C L^-1, 총질소 농도는 각각 2.5±0.6, 3.5±0.5, 3.1±0.8 mg N L^-1, 총인 농도는 각각0.12±0.03, 0.11±0.02, 0.16±0.02 mg P L^-1였다.

Results and Discussion

시나리오 1: 추적자 종류와 개수에 따른 SIAR 모형의 정확도

시나리오 1에서 오염원을 5개로 고정하고 각 오염원의 기여도가 상이한 3개의 유역 (Sink 1–3) (Table 2b)을 대상으로 추적자의 종류와 수를2‒5개로 달리하여 SIAR 모형의 정확도를 검토한 결과, end-member 개수가 2개일 경우 (Combination A), 설정치와 예측치의 차이가 -22 ~ +22%로 오염원 기여도 평가의 정확도가 낮았다 (Table 4). 이는 오염원 기여도 설정치와 예측치의 회귀 분석 결과에서r²이 0.00 - 0.56으로 낮은 것으로도 확인되었다 (Fig. 2a). 반면, 3개의 end-member (Combination B-D)를 활용하면 오염원의 기여도의 정확도가 증가하였다. 비록Combination C의 경우, 설정치–예측치 회귀식의 r²이 0.65 (Sink 3)이하로 낮았지만, Combination B와 D에서는 대부분의 r²이 0.90 이상으로 높아 예측치의 정확도가 향상되었다 (Fig. 2b-d). 또한, 4개의 end-member (Combination E-G)를 사용하면 설정치–예측치 회귀식의 r²이 일부를 제외하고 0.92‒0.99로 높았다 (Fig. 2e-g). 하지만, 3개의 end-member를 활용한 Combination D와 4개의 end-member를 활용한 Combination F에서 Sink 3에 대한 설정치–예측치 회귀식의 r²이 각각 0.55와 0.34로 낮은 점은 SIAR 모형의 정확도가 end-member 개수에 결정되지 않음을 보여준다. 일반적으로, 오염원 개수가 n개일 때 SIAR 모형 구동을 위해서 n-1개의 end-member가 필요하지만 (Parnell, 2008), 본 연구 결과는 end-member의 개수는 물론 해당 end-member의 오염원 대표성 역시 중요함을 제시한다. 예를 들면, 시나리오1에서 Sink 3의 경우 상대적으로 산림의 기여도가 큰 데에 반해 (Table 4), Combination D와 F에는 산림유출수의 특성을 보여 줄 수 있는 N/P가 end-member로 포함되지 않았다 (Table 4). 일반적으로 인산질 비료가 시용 되지 않으면서, 대기로부터 질소강하물이나 질소 고정과 같은 경로로 질소가 유입되는 산림은 농경지 등의 타 오염원에 비해서 N/P가 높은 것으로 알려져 있다 (Jeon et al., 2015; Shen et al., 2019; Choi et al., 2020).

Fig. 2

Correlation between the given and SIAR-estimated contributions of sources to a sink under the Scenario 1 with fixed contribution of sources and varying combinations of tracers (Table 2): (a) end-members δ13C-δ15N, (b) end-members δ¹³C-δ¹⁵N-C/N, (c) end-members δ¹³C-δ¹⁵N-N/P, (d) end-members δ¹³C-δ¹⁵N-Na/Ca, (e) end-members δ¹³C-δ¹⁵N-C/N-N/P, (f) end-members δ¹³C-δ¹⁵N-C/N-Na/Ca, (g) end-members δ¹³C-δ¹⁵N-N/P-Na/Ca, and (h) end-members δ¹³C-δ¹⁵N-C/N-N/P-Na/Ca. Data depicted in the figure are provided in Table 4.

한편, 5개의 오염원에 대해 5개의 end-member를 활용한 Combination H에서는 설정치–예측치 회귀식의 r²이 0.94‒0.98로 매우 높았다 (Fig. 2h). 따라서, 이상의 결과를 종합하면, 추적자의 오염원 대표성이 높을 경우에는 n개의 오염원에 대해 (n-1)개의 end-member로 신뢰도 높은 오염원 기여도 평가가 가능하지만, 추적자에 대한 신뢰도가 낮을 경우에는 가급적 다수의 end-member를 사용하면 오염원 평가의 정확도가 향상되는 것을 알 수 있다 (Parnell, 2008).

시나리오 2: 오염원 개수가 상이한 조건에서 각 오염원의 기여도 변화에 따른 SIAR 모형의 정확도

시나리오 2에서 오염원의 종류가 3‒5개인 조건에서 추적자를 5개로 고정하고, 오염원의 오염 기여도가 5가지로 변하는 조건에서 SIAR의 정확도를 평가한 결과, SIAR의 오염원 평가 정확도는 오염원 개수와 end-member 개수의 조합은 물론, 오염원별 기여도 변화에 의해서도 달라지는 것으로 나타났다 (Table 5). 예를 들면, 오염원이 각각 3개와 4개인 조건에서 오염원별 기여도 설정치가 각각 30%내외와 20% 내외로 유사한 경우 (각각 Type 3과 5), SIAR의 예측치는 설정치와 정확하게 일치하였다. 하지만, 오염원이 5개인 조건에서 오염원별 기여도 설정치가 유사한 Type 5의 예측치는 설정치와 -13 ~ +8의 차이가 있었고 (Table 5), 설정치와 예측치 회귀분석의r²이 0.09로 매우 낮았다 (Fig. 3). 또한, 오염원이 5개인 조건에서 Type 4의 r²도 0.54로 매우 낮았다. 한편, 오염원 보다 더 많은 end-members를 활용한 조건에서 r²이 0.90 이상으로 높았다. 이러한 결과는 오염원 개수 보다 많은 수의 end-member를 활용하면 오염원의 기여도가 다양하게 변하더라도 SIAR 모형 예측 결과가 상대적으로 정확함을 보여준다 (Parnell, 2008). 따라서, SIAR을 활용한 오염원 기여도 평가의 정확도 확보를 위해서는 가급적 많은 end-member를 활용할 필요가 있다.

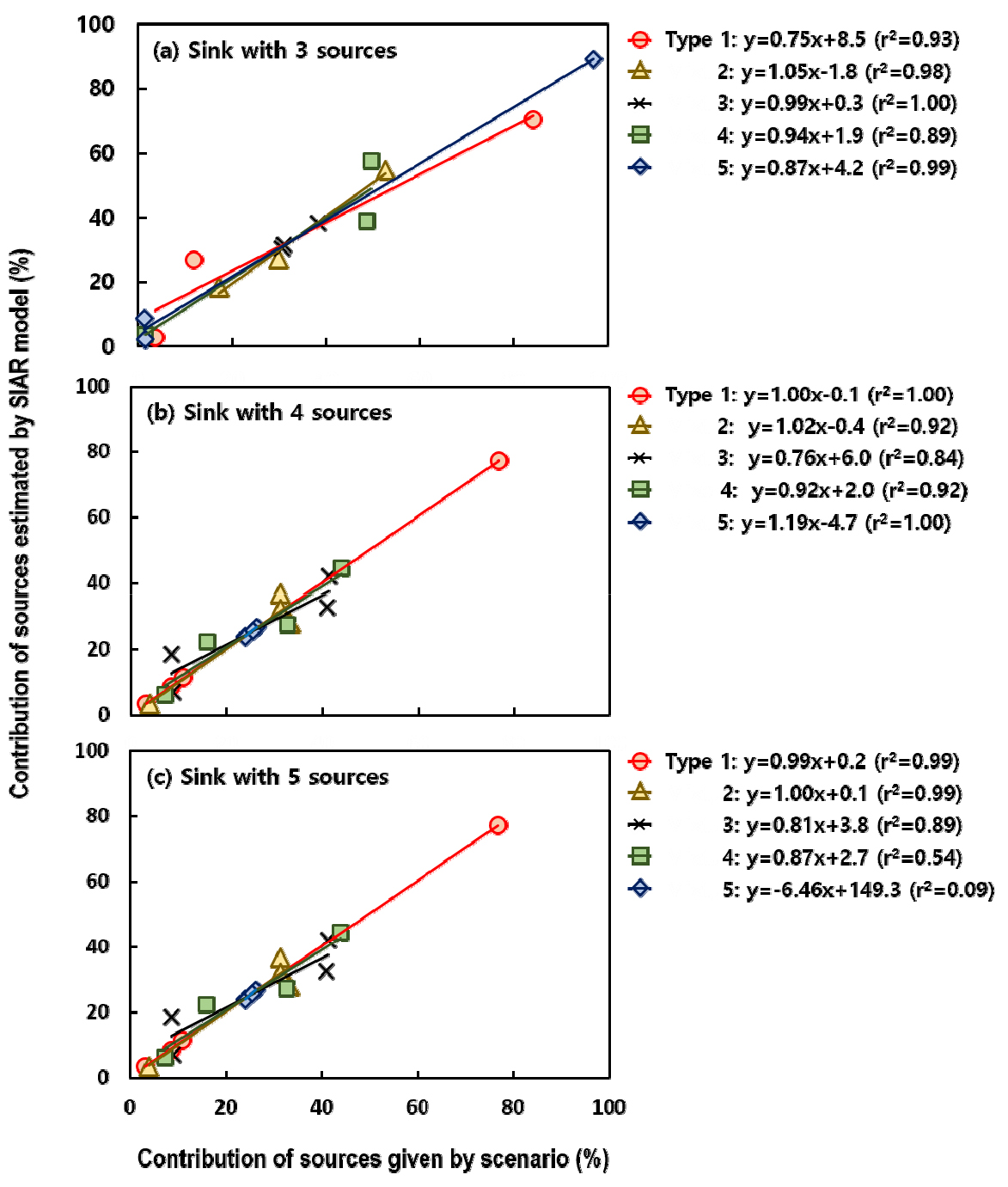
Fig. 3

Correlation between the given and SIAR-estimated contributions of sources to a sink under the Scenario 2 with varying number of sources (3‒5) and their contribution and fixed 5 tracers (Table 2): (a) sink with 3 sources, (b) sink with 4 sources, and (c) sink with 5 sources. Data depicted in the figure are provided in Table 4.

실제 유역을 대상으로 한 SIAR 적용

Jeon (2015)의 실측 자료를 활용하여 SIAR 모형을 적용한 결과에 의하면, 오염원 별 기여도는 총탄소의 경우 과수원 (22%) > 산림 (20%) > 논 (21%) > 밭 (19%) > 주거 (18%)의 순서였고, 총질소는 산림 (37%) > 주거 (28%) > 밭 (21%) > 논=과수원 (7%), 총인은 산림 (23%) > 과수원=밭=주거 (20%) > 논 (17%)의 순서였다 (Fig. 4). 실제 오염원 별 기여도에 대한 신뢰도가 확보된 결과가 없기 때문에 본 연구의 오염원 평가 결과의 정확도를 평가하기는 어렵다. 하지만, 본 연구에서는 전체 오염원이 5개였고, end-member는 총탄소 (C/N, C/P, δ¹³C)와 총질소 (C/N, N/P, δ¹⁵N)는 3개, 총인 (N/P, C/P)은 2개를 사용하여, SIAR 모형의 기본 end-member (n-1)인 4개보다 적었기 때문에 오염원 기여도 평가의 정확도는 낮을 것으로 판단된다 (Parnell, 2008). 하지만, SIAR의 사례 연구 적용을 통해 SIAR의 활용 가능성을 확인하였다는 측면에서 연구 결과의 의미를 찾을 수 있다. 앞의 시나리오별 SIAR 모형 결과에 의하면 총탄소, 총질소, 총인의 오염원 별 특징적 추적자와 해당 end-member를 추가하면 오염원 별 기여도 평가 결과의 정확도를 높일 수 있을 것으로 기대된다.

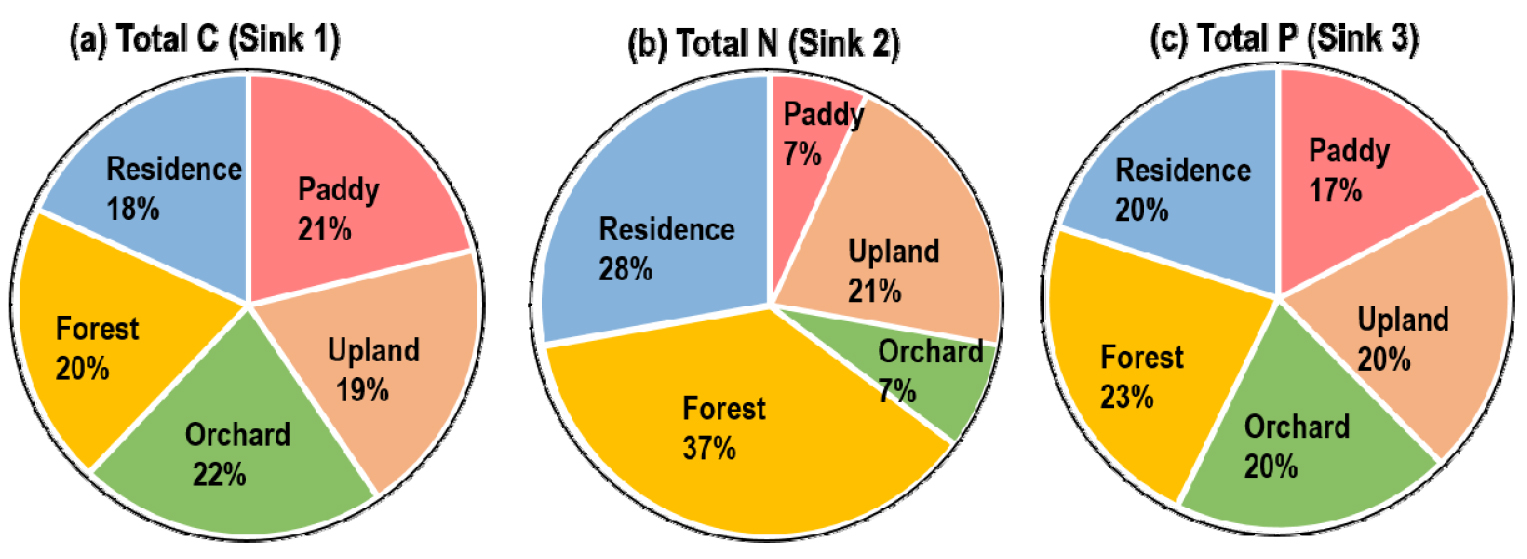
Fig. 4

Contribution of source to sink (water samples) with different water chemistry: (a) total C of sink 1, (b) total N of sink 2, and (c) total P of sink 3. Details of water chemistry are provided in Table 3.

Conclusions

SIAR 모형은 지금까지 전세계에서 수질 오염원을 추적하기 위한 연구에 활용되어 왔지만, 복합토지이용 유역의 수질 오염원을 추적하기 위한 SIAR 모형의 정확성이 검증된 바 없어 산출된 오염원의 기여도에 대한 신뢰도를 향상시킬 필요가 있다. 본 연구에서 시나리오별로SIAR 모형의 오염원 기여도 평가 정확도를 검증한 결과, n개의 오염원에 대한 정확한 오염 기여도 평가를 위해서는 최소 n-1개의 end-member가 필요하지만, end-member로 사용된 추적자가 오염원의 특성을 제대로 반영하지 못할 때는 오염 기여도의 정확도가 낮아지는 것으로 나타났다. 따라서, 추적자의 오염원 별 대표성이 불확실할 경우에는 오염원 개수와 동일하거나 많은 end-member를 사용하면 이와 같은 문제를 극복할 수 있는 것으로 나타났다. SIAR의 사례연구 적용 결과에 의하면, 총탄소, 총질소, 총인 오염에 대한 오염원 별 기여도 결과의 정확도를 평가할 수는 없었지만, SIAR을 이용한 오염원 기여도 평가 가능성은 확인할 수 있었다. 향후 주요 오염물질 별 오염원의 특징을 대표할 수 있는 추가적인 추적자와 해당 end-member를 보완하면 보다 정확한 오염원 평가가 가능할 것으로 기대된다.